练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，AD=4，CD=3，∠ADC=90°，AB=13，∠ACB=90°，求图形中阴影部分的面积．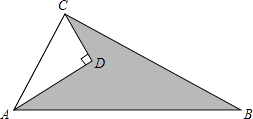

    【答案】解：在Rt△ACD中，AC= =5； 在Rt△ACD中，BC= =12；
    ∴S△ABC= ×5×12=30，
    S△ACD= ×4×3=6，
    ∴阴影部分面积为30﹣6=24
    【解析】根据勾股定理求出AC的长，再根据勾股定理求出BC的长，求出△ABC的面积，再求出△ACD的面积，相减即可．
    【考点精析】关于本题考查的勾股定理的概念和勾股定理的逆定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是 边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算（直接写出结果）:①a·a3=__________． ②(b3)4=________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用2，3，4，5这四个数字，使计算的结果为24，请列出1个符合要求的算式____________（可运用加、减、乘、除、乘方）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1,在△ABC中,以AB为直径作⊙O分别交AC，BC于点D，E，且

    （1）求证：AB=AC.

    （2）若∠C=70°，求的度数.

    （3）如图2，点F在⊙O上， ，连结DF，DE.求证：∠ADF=∠CDE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于的二次函数y=x2+2kx+k-1，下列说法正确的是（ ）

    A. 对任意实数k，函数与x轴都没有交点

    B. 存在实数n，满足当时，函数y的值都随x的增大而减小

    C. 不存在实数n，满足当时，函数y的值都随x的增大而减小

    D. 对任意实数k，抛物线都必定经过唯一定点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）
    A.a2a3=a6
    B.2a+3a=6a
    C.a2+a2+a2=3a2
    D.a2+a2+a2=a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图5—13，在△ABC中，AD⊥BC，GC⊥BC，CF⊥AB，BE⊥AC，垂足分别为D、C、F、E，则_______是△ABC中BC边上的高，_________是△ABC中AB边上的高，_________是 △ABC中AC边上的高，CF是△ABC的高，也是△_______、△_______、△_______、△_________的高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

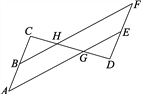
    【题目】如图所示，已知B、E分别是线段AC、DF的中点，AC=DF，BF交CD于点H，AE交CD于点G，CH=HG=DG，BH=GE.

    (1)填空：因为B、E分别是线段AC、DF的中点，所以CB=________AC，DE=________DF.因为AC=DF，所以CB=________.在△CBH和△DEG中，因为CB=________，CH=________，BH=________EG，所以________≌________(SSS)．

    (2)除了(1)中的全等三角形外，请你再写出另外一对全等三角形，并说明理由．

    查看答案和解析>>

    同步练习册答案