
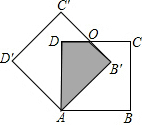
 如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.
如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$. 分析 此题只需把公共部分分割成两个三角形,根据旋转的旋转发现两个三角形全等,从而求得直角三角形的边,再进一步计算其面积.
解答 解:如图,连接AO,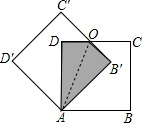
根据旋转的性质,得∠BAB′=30°,则∠DAB′=60°.
在Rt△ADO和Rt△AB′O中,AD=AB′,AO=AO,
∴Rt△ADO≌Rt△AB′O.
∴∠OAD=∠OAB′=30°.
又∵AD=1,
∴OD=AD•tan∠OAD=$\frac{\sqrt{3}}{3}$.
∴阴影部分的面积=2×$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$×1=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了旋转的性质,正方形的性质,全等三角形判定与性质,解直角三角形,利用全等三角形求出∠DAO=∠B′AO,从而求出∠DA0=30°是解题的关键,


科目:初中数学 来源: 题型:解答题
 (1)完成下面的证明.
(1)完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
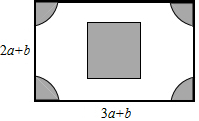 如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a-b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-$\sqrt{3}$x+$\frac{1}{2}$=0 | B. | x2+$\sqrt{3}$x+$\frac{1}{2}$=0 | C. | x2-$\sqrt{3}$x+1=0 | D. | x2+$\sqrt{3}$x-$\frac{1}{2}$=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
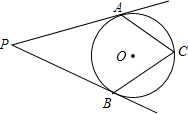 如图,PA,PB是⊙O的切线,切点分别为A,B,C在⊙O上,则∠P与∠C的关系是( )
如图,PA,PB是⊙O的切线,切点分别为A,B,C在⊙O上,则∠P与∠C的关系是( )| A. | 2∠P+∠C=180° | B. | 2∠P+∠C=360° | C. | ∠P+2∠C=180° | D. | ∠P+∠C=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.设甲、乙两人间的距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,下列结论中,错误的是( )
甲骑摩托车从A地去B地.乙开汽车从B地去A地.同时出发,匀速行驶.各自到达终点后停止.设甲、乙两人间的距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,下列结论中,错误的是( )| A. | 出发1小时时,甲、乙在途中相遇 | |
| B. | 出发1.5小时时,乙比甲多行驶了60千米 | |
| C. | 出发3小时时,甲、乙同时到达终点 | |
| D. | 甲的速度是乙速度的一半 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com