
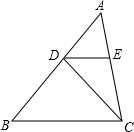
 如图,在△ABC中,AB=4,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值为$\frac{1}{4}$.
如图,在△ABC中,AB=4,D是AB上的一点(不与点A、B重合),DE∥BC,交AC于点E,则$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值为$\frac{1}{4}$. 分析 设AD=x,$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$=y,求出$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{16}$x2①,$\frac{{S}_{△ADE}}{{S}_{△DEC}}$=$\frac{AE}{EC}$=$\frac{x}{4-x}$②,①÷②即可得出y关于x的函数关系式以及自变量x的取值范围,于是得到y=$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x=-$\frac{1}{16}$(x-2)2+$\frac{1}{4}$≤$\frac{1}{4}$,即可得到结论.
解答 解:设AD=x,$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$=y,
∵AB=4,AD=x,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=($\frac{x}{4}$)2,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{16}$x2①,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,
∵AB=4,AD=x,
∴$\frac{AE}{AC}$=$\frac{x}{4}$,
∴$\frac{AE}{CE}$=$\frac{x}{4-x}$,
∵△ADE的边AE上的高和△CED的边CE上的高相等,
∴$\frac{{S}_{△ADE}}{{S}_{△DEC}}$=$\frac{AE}{EC}$=$\frac{x}{4-x}$②,
①÷②得:
∴y=$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$=-$\frac{1}{16}$x2+$\frac{1}{4}$x,
∵AB=4,
∴x的取值范围是0<x<4;
∴y=$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$=-$\frac{1}{16}$(x-2)2+$\frac{1}{4}$≤$\frac{1}{4}$,
∴$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值为$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题主要考查了相似三角形的性质和判定,三角形的面积的计算方法,二次函数的最值问题,熟练掌握相似三角形的判定和性质定理是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
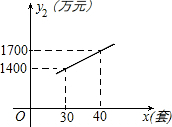 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB为⊙O的直径,AB=4$\sqrt{3}$,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
如图,AB为⊙O的直径,AB=4$\sqrt{3}$,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )| A. | 随点C的运动而变化,最大值为4 | B. | 随点C的运动而变化,最大值为4$\sqrt{3}$ | ||
| C. | 随点C的运动而变化,最小值为2 | D. | 随点C的运动而变化,但无最值 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com