练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知直线与双曲线交于A、B两点，点B坐标为(-4,-2)，C为双曲线上一点，且在第一象限内，若△AOC面积为6，则点C坐标为（ ）

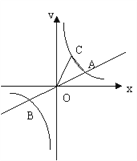
    A. （4,2） B. （2,3） C. （3,4） D. （2,4）

    【答案】D

    【解析】

    ∵点B(4,2)在双曲线上， ，∴k=8.

    ∵点A，点B关于原点对称，所以A(4,2)，

    如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为 ，

    若S△AOC=S△COF+S梯形ACFE-S△AOE .∵△AOC的面积为6， ，整理得,a2+6a16=0，

    解得a1=2,a2=8(舍去)，∴点C的坐标为(2,4).

    作AE⊥x于点E, CF⊥x于点F.

    S△AOC=S△AOE+S梯形ACFES△COF.

    ∵△AOC的面积为6， ，即 .

    解之得：a=8或a=2(舍去)

    ∴点C的坐标为(8,1).

    故答案为：(2,4)或(8,1).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，可是小红这两道题都不会，不过竞赛规则规定每位选手有两次求助机会，使用“求助”一次可以让主持人去掉其中一题的一个错误选项，主持人提醒小红可以使用两次“求助”．

    (1)如果小红两次“求助”都在第一道题中使用，那么小红通关的概率是 .

    (2)如果小红将每道题各用一次“求助”，请用树状图或者列表来分析她顺序通关的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，以BC为直径的半圆O交斜边AB于点 D．

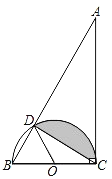
    （1）证明：AD＝3BD；

    （2）求弧BD的长度；

    （3）求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形纸片沿折叠，使点与点重合，再将沿折叠，使点恰好落在上的点处．若，则的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某几何体的三视图及相关数据，则该几何体的表面积是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知⊙O中，AB为弦，直线PO交⊙O于点M、N，PO⊥AB于C，过点B作直径BD，连接AD、BM、AP．

    （1）求证：PM∥AD；

    （2）若∠BAP=2∠M，求证：PA是⊙O的切线；

    （3）若AD=6，tan∠M=，求⊙O的直径．

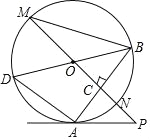
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两车分别从A、B两地同时出发，在同一条公路上，匀速行驶，相向而行，到两车相遇时停止.甲车行驶一段时间后，因故停车0.5小时，故障解除后，继续以原速向B地行驶，两车之间的路程y（千米）与出发后所用时间x(小时）之间的函数关系如图所示.

    （1）求甲、乙两车行驶的速度V甲、V乙.

    （2）求m的值.

    （3）若甲车没有故障停车，求可以提前多长时间两车相遇.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某乡镇实施产业精准扶贫，帮助贫困户承包了若干亩土地种植新品草莓，已知该草莓的成本为每千克10元，草莓成熟后投入市场销售，经市场调查发现，草莓销售不会亏本，且每天的销售量y（千克）与销售单价x（元/千克）之间函数关系如图所示．

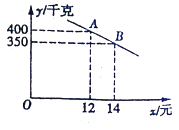
    （1）求y与x的函数关系式，并写出x的取值范围．

    （2）当该品种草莓的定价为多少时，每天销售获得利润最大？最大利润是多少？

    （3）某村今年草莓采摘期限30天，预计产量6000千克，则按照（2）中的方式进行销售，能否销售完这批草莓？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

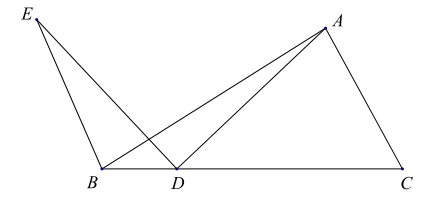
    【题目】如图，在中，点是线段上的动点，将线段绕点逆时针旋转得到线段，连接．若已知，设两点间的距离为两点间的距离为两点间的距离为．（若同学们打印的BC的长度如不是，请同学们重新画图、测量）

    小明根据学习函数的经验，分别对自变量x的变化而变化的规律进行了探究，下面是小明的探究过程，请补充完整：

    （1）按照下表中自变量的值进行取点、画图、测量，分别得到了与的几组对应值，如下表：

    0

    1

    2

    3

    4

    5

    6

    7

    8

    7.03

    6.20

    5.44

    4.76

    4.21

    3.85

    3.73

    3.87

    4.26

    5.66

    4.32

    1.97

    1.59

    2.27

    3.43

    4.73

    写出的值．（保留1位小数）

    （2）在同一平面直角坐标系中，描出补全后的表中各组数值所对应的点，并画出函数的图象；

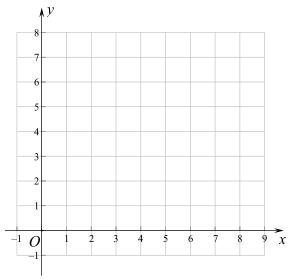
    （3）结合函数图像，解决问题：

    ①当在线段上时，的长度约为________；

    ②当为等腰三角形时，的长度约为_______．

    查看答案和解析>>

    同步练习册答案