
分析 根据方程有两个实数根结合根的判别式即可得出△=8k+8≥0,解之即可得出k的取值范围,再结合根与系数的关系以及x1+x2<x1x2,即可得出4<2-2k,解之即可得出k的取值范围,取两个k的取值范围的交集即可得出结论.
解答 解:不存在,理由如下:
∵方程x2-4x-2(k-1)=0有两个实数根x1,x2,
∴△=(-4)2-4×1×[-2(k-1)]=8k+8≥0,
解得:k≥-1.
∵x1+x2=4,x1x2=2-2k,x1+x2<x1x2,
∴4<2-2k,
解得:k<-1.
∵k≥-1和k<-1没有交集,
∴不存在x1+x2<x1x2的情况.
点评 本题考查了根的判别式以及根与系数的关系,根据根的判别式以及根与系数的关系找出关于k的一元一次不等式是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于2.4.
如图,在△ABC中,∠ACB=90°,AC=6,BC=8,点D是斜边AB上任意一点,DE⊥AC,DF⊥BC,垂足分别是点E、F,点Q是EF的中点,则线段DQ长的最小值等于2.4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | 1 | 2 | 3 | 4 |
| x2-2x-2 | -3 | -2 |
| x | 2.6 | 2.7 | 2.8 | 2.9 |
| x2-2x-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
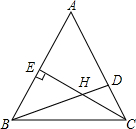 如图,在△ABC中,∠ABC=50°,∠ACB=70°,BD是∠ABC的平分线,CE是AB边上的高线,BD与CE交于点H,求∠ADB和∠BHC的度数.
如图,在△ABC中,∠ABC=50°,∠ACB=70°,BD是∠ABC的平分线,CE是AB边上的高线,BD与CE交于点H,求∠ADB和∠BHC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com