
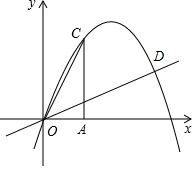
 如图,过A(1,0)作x轴的垂线,交抛物线y=-$\frac{4}{3}$x2+$\frac{13}{3}$x于点C.D(3,a)为抛物线上一点,点M为线段OD上的一个动点,MN∥AC交抛物线于点N.
如图,过A(1,0)作x轴的垂线,交抛物线y=-$\frac{4}{3}$x2+$\frac{13}{3}$x于点C.D(3,a)为抛物线上一点,点M为线段OD上的一个动点,MN∥AC交抛物线于点N.分析 (1)把D(3,a)代入抛物线的解析式求得a的值,然后设直线OD的解析式为y=kx,代入D的坐标,根据待定系数法即可求得;
(2)求得C的坐标,然后根据题意设出点M的坐标,表示出点N坐标,以A、C、M、N为顶点的四边形为平行四边形只要AC=MN,用它建立方程求出m,进而求得M的坐标即可.
解答 解:(1)∵D(3,a)为抛物线上一点,
∴a=-$\frac{4}{3}$×32+$\frac{13}{3}$×3=1,
∴D(3,1)
设直线OD的解析式为y=kx,代入D的坐标得:1=3k,
∴k=$\frac{1}{3}$,
∴直线OD的解析式为y=$\frac{1}{3}$x;
(2)过A(1,0)作x轴的垂线,交抛物线y=-$\frac{4}{3}$x2+$\frac{13}{3}$x于点C,
∴把x=1代入得,y=3,
∴C(1,3),
∴AC=3,
∵点M为直线OD上的一个动点,
∴设M(m,$\frac{1}{3}$m),
∴N(m,-$\frac{4}{3}$m2+$\frac{13}{3}$m),
∴MN=|-$\frac{4}{3}$m2+$\frac{13}{3}$m-$\frac{1}{3}$m|=$\frac{1}{3}$|-4m2+12m|,
∵四边形ACNM为平行四边形,
∴AC=MN,
∴$\frac{1}{3}$|-4m2+12m|=3,
∵0<m<4,
∴-4m2+12m>0,
∴-4m2+12m=9,
∴m=$\frac{3}{2}$,
把x=m=$\frac{3}{2}$代入y=-$\frac{4}{3}$x2+$\frac{13}{3}$x得n=$\frac{7}{2}$
∴M($\frac{3}{2}$,$\frac{7}{2}$).
点评 此题考查了待定系数法求直线的解析式,二次函数图象上点的坐标特征,平行四边形的性质,求得点的坐标是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
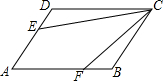 如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=$\frac{263}{24}$cm.
如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF=$\frac{263}{24}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com