
【题目】如图,点A(1,3)、点B(m,1)是一次函数![]() 的图像上的两点,一次函数
的图像上的两点,一次函数![]() 图像与x轴交于点D.
图像与x轴交于点D.

(1)b = ,m = ;
(2)过点B作直线l垂直于x轴,点E是点D关于直线l的对称点,点C是点A关于原点的对称点.试判断点B、E、C是否在同一条直线上,并说明理由.
(3)连结AO、BO,求△AOB的面积;
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
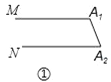
【题目】下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2=______度,
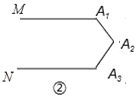
图②中的∠A1+∠A2+∠A3=______度,
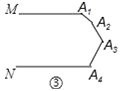
图③中的∠A1+∠A2+∠A3+∠A4=______度,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=______度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An=______.
(3)证明图②中的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据条件画图,并回答问题:
(1)画一个锐角△ABC(三边均不相等);
(2)画出BC边上的中线AE和高AD;
(3)写出所有以AD为高的三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班组织班团活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品,已知笔记本2元/本,中性笔1元/支,且每种奖品至少买1件.
(1)若设购买笔记本x本,中性笔y支,写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
(3)从上述方案中任选一种方案购买,求买到的中性笔与笔记本数量相等的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
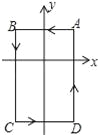
A. (1,﹣1) B. (﹣1,1) C. (﹣1,﹣2) D. (1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
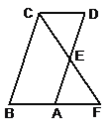
【题目】如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会会期为2010年5月1日至2010年10月31日。门票设个人票和团队票两大类。个人普通票160元/张,学生优惠票100元/张;成人团队票120元/张,学生团队票50元/张。
(1)如果2名老师、10名学生均购买个人票去参观世博会,请问一共要花多少元钱购买门票?
(2)用方程组解决下列问题:如果某校共30名师生去参观世博会,并得知他们都是以团队形式购买门票,累计花去2200元,请问该校本次分别有多少名老师、多少名学生参观世博会?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= ![]() 的图象经过D点.
的图象经过D点.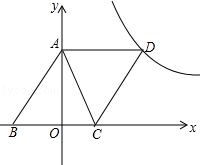
(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y= ![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com