
【题目】已知:如图,⊙O是△ABC的内切圆,下列说法错误的是( )
A.点O在△ABC的三边垂直平分线上
B.点O在△ABC的三个内角平分线上
C.如果△ABC的面积为S,三边长为a,b,c,⊙O的半径为r,那么r=![]()
D.如果△ABC的三边长分别为5,7,8,那么以A、B、C为端点三条切线长分别为5,3,2
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.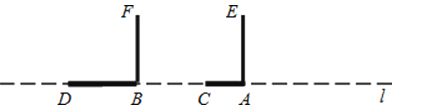
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB.
求证:CA+AD=BC.
小明为解决上面的问题作了如下思考:作△ADC关于直线CD的对称图形△A′DC,
∵CD平分∠ACB,∴A′点落在CB上,且CA′=CA,A′D=AD.因此,要证的问题转化为只要证A′D=A′B.请根据小明的思考写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
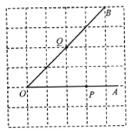
【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家居专营店用2730元购进A、B两种新型玻璃保温杯共60个,这两种玻璃保温杯的进价、标价如表所示:
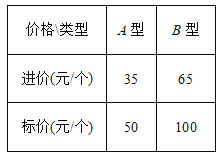
(1)这两种玻璃保温杯各购进多少个?
(2)若A型玻璃保温杯按标价的9折出售,B型玻璃保温杯按标价的8.5折出售,且在运输过程中有2个A型、1个B型玻璃保温杯不慎损坏,不能进行销售,请问这批玻璃保温杯全部售出后,该家居专营店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧AB上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则△PDE的周长是( )
A.4
B.8
C.12
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3x2+3y2﹣5xy,B=2xy﹣3y2+4x2.
(1)化简:2B﹣A;
(2)已知﹣a|x﹣2|b2与![]() aby的同类项,求2B﹣A的值
aby的同类项,求2B﹣A的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com