
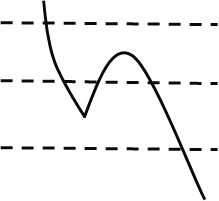
【题目】在平面直角坐标系中,点![]() 在抛物线上,将抛物线
在抛物线上,将抛物线![]() 在点
在点![]() 右侧的部分沿着直线
右侧的部分沿着直线![]() 翻折,翻折后的图象与原抛物线剩余部分合称为图象
翻折,翻折后的图象与原抛物线剩余部分合称为图象![]() .
.
(1)当![]() 时,
时,
①在如图的平面直角坐标系中画出图象![]() ;
;
②直接写出图象![]() 对应函数的表达式;
对应函数的表达式;
③当![]() 时,图象
时,图象![]() 对应函数的最小值为
对应函数的最小值为![]() 求
求![]() 的取值范围.
的取值范围.
(2)当![]() 时,直接写出图象
时,直接写出图象![]() 对应函数
对应函数![]() 随
随![]() 增大而减小时
增大而减小时![]() 的取值范围.
的取值范围.
(3)若图象![]() 上有且只有三个点到直线
上有且只有三个点到直线![]() 的距离为
的距离为![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)①作图见解析;②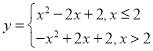 ;③
;③![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)①先画出翻折之前的抛物线,再把![]() 的部分沿着直线
的部分沿着直线![]() 翻折即可;
翻折即可;
②翻折之后的图象形状不变,开口向下,再利用待定系数法即可解决问题;
(2)画出当![]() 时的图象G,根据图象分析即可;
时的图象G,根据图象分析即可;
(3)利用数形结合的思想,画出图象,分类讨论即可.
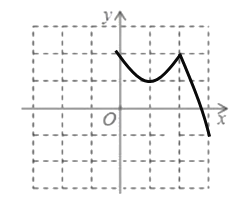
(1)①当![]() 时,抛物线解析式为:
时,抛物线解析式为:![]() ,则
,则![]() ,因此翻折后的图象如图:
,因此翻折后的图象如图:
②当![]() 时为解析式为
时为解析式为![]() ,
,
沿![]() 翻折之后,开口向下,形状不变,故设翻折之后的解析式为:
翻折之后,开口向下,形状不变,故设翻折之后的解析式为:![]() ,将点
,将点![]() ,
,![]() 代入可得:
代入可得:![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() ,故图象
,故图象![]() 对应函数的表达式为:
对应函数的表达式为: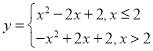
③把![]() 代入
代入![]() 得
得![]() ,
,
∵![]() ,
,
![]()
![]() ;
;
(2)当![]() 时,原函数
时,原函数![]() 的顶点坐标为
的顶点坐标为![]() ,故图象G如图:
,故图象G如图:
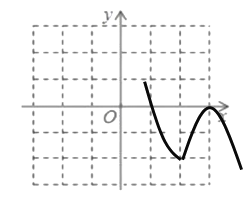
根据图象可知![]() 随
随![]() 增大而减小时
增大而减小时![]() 的取值范围为:
的取值范围为:![]() 或
或![]() ;
;
(3)点![]() 在抛物线
在抛物线![]() 上,故
上,故![]() ,翻折之前的顶点坐标为
,翻折之前的顶点坐标为![]() ,翻折之后的解析式为
,翻折之后的解析式为![]() ,翻折之后的顶点坐标为
,翻折之后的顶点坐标为![]() ,
,
①当点A在对称轴右侧时,即![]() 时:
时:
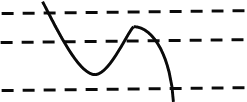
若直线![]() 在点A上方,则只需让点A到直线
在点A上方,则只需让点A到直线![]() 的距离为3即可,即
的距离为3即可,即![]() ,解得:
,解得:![]() (舍);
(舍);
若直线![]() 在点A下方,且在翻折前顶点的上方,则需让
在点A下方,且在翻折前顶点的上方,则需让![]() 的顶点和点A到直线
的顶点和点A到直线![]() 的距离一个刚好等于3,一个小于3即可,即
的距离一个刚好等于3,一个小于3即可,即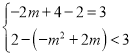 或
或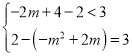 ,解得:
,解得:![]() ;
;
若直线![]() 在翻折前顶点的下方,则只需让翻折前顶点到直线
在翻折前顶点的下方,则只需让翻折前顶点到直线![]() 的距离 3即可,即
的距离 3即可,即![]() ,此时无解;
,此时无解;
②当点A在对称轴左侧时,即![]() 时:
时:
若直线![]() 在翻折后顶点的上方,则只需让翻折后顶点到直线
在翻折后顶点的上方,则只需让翻折后顶点到直线![]() 的距离 3即可,即
的距离 3即可,即![]() ,解得
,解得![]() (舍);
(舍);
若直线![]() 在点A上方,且在翻折后顶点的下方,则需让
在点A上方,且在翻折后顶点的下方,则需让![]() 的顶点和点A到直线
的顶点和点A到直线![]() 的距离一个刚好等于3,一个小于3即可,即
的距离一个刚好等于3,一个小于3即可,即 或
或 ,解得:
,解得:![]() ;
;
若直线![]() 在点A下方,则只需让点A到直线
在点A下方,则只需让点A到直线![]() 的距离为3即可,此时
的距离为3即可,此时![]() ;
;
综上所述,m的值为:![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
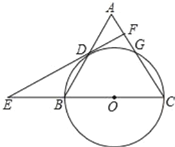
【题目】如图,在![]() ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
ABC中,CA=CB=10,AB=12,以BC为直径的圆⊙O交AC于点G,交AB于点D,过点D作⊙O的切线,交CB的延长线于点E,交AC于点F.则下列结论正确的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,他们的形状、大小、质地等完全相同.小兰先从盒子里随机取出一个小球,记下数字为x,放回盒子,摇匀后,再由小田随机取出一个小球,记下数字为y
(1)用列表法或画树状图法表示出(x,y)的所有可能出现的结果;
(2)求小兰、小田各取一次小球所确定的点(x,y)落在反比例函数![]() 的图象上的频率;
的图象上的频率;
(3)求小兰、小田各取一次小球所确定的数x,y满足![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为一幢高3米的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方的点A处建一幢高12米的楼房AB.(设A,C,F在同一水平线上)
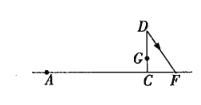
(1)作出楼房AB及它的最大影长AE;
(2)楼房AB建成后,其是否影响温室CD的采光?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013-2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营业、收入比例情况统计图(数据来源:公司财报、中商产业研究院).
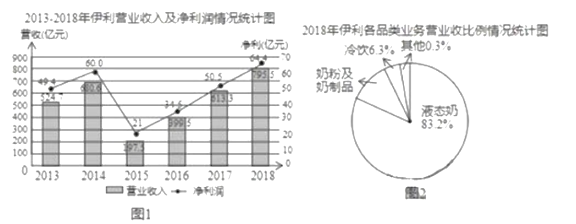
综合实践小组的同学结合统计图提出了如下问题,请你解答:
(1)2018年,伊利集团营收及净利再次刷新行业记录,稳居亚洲乳业第一,这一年,伊利集团实现营业收入 亿元,净利润 亿元.
(2)求2018年伊利集团“奶粉及奶制品”业务的营业收入(结果精确到![]() 亿元).
亿元).
(3)在2013-2018这![]() 年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
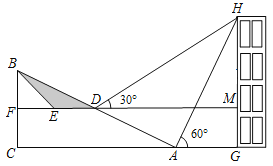
【题目】如图,坡AB的坡度为1:2.4,坡面长26米,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(请将下面两小题的结果都精确到0.1米,参考数据:![]() ≈1.732).
≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)恰为45°,则此时平台DE的长为 米;
(2)坡前有一建筑物GH,小明在D点测得建筑物顶部H的仰角为30°,在坡底A点测得建筑物顶部H的仰角为60°,点B、C、A、G、H在同一平面内,点C、A、G在同一条水平直线上,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
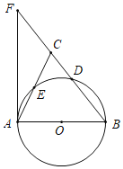
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E时![]() 的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=10.tan∠FAC=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
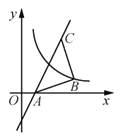
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,AB=5,AC=6,AC的平行线DE交BC的延长线于点E,则四边形ACED的面积为______.
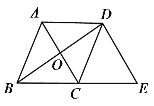
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com