
分析 (1)运用整式乘除法将原式展开后、再合并同类项后,将a、b代入求值即可;
(2)运用平方差公式和完全平方公式将原式化简即可.
解答 解:(1)原式=-9a4+18a3b-(3b2+4a3b)
=-9a4+18a3b-3b2-4a3b
=-9a4+14a3b-3b2,
当a=-1,b=-2时,
原式=-9×(-1)4+14×(-1)3×(-2)-3×(-2)2
=-9+28-12
=7;
(2)原式=[(a+3)(a-3)]2-[a2-(a-3)][a2+(a-3)]
=(a2-9)2-[a4-(a-3)2]
=a4-18a2+81-a4+a2-6a+9
=-17a2-6a+90.
点评 本题主要考查整式的混合运算,熟练掌握整式的运算法则和完全平方公式、平方差公式是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
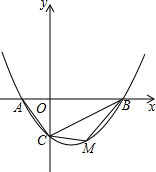 如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,已知B点坐标为(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x(元/kg) | … | 70 | 75 | 80 | 85 | 90 | … |
| 月销售量y(kg) | … | 100 | 90 | 80 | 70 | 60 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 用电量(度) | 120 | 140 | 160 | 180 | 200 |
| 户数 | 2 | 3 | 6 | 7 | 2 |
| A. | 180,180 | B. | 160,180 | C. | 160,160 | D. | 180,160 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
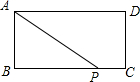 如图,在矩形ABCD中,AB=2,AD=4,矩形边上一动点P沿A→B→C→D→A的路径移动.设点P经过的路径长为x,AP2=y,则下列能大致反映y与x的函数关系的图象是( )
如图,在矩形ABCD中,AB=2,AD=4,矩形边上一动点P沿A→B→C→D→A的路径移动.设点P经过的路径长为x,AP2=y,则下列能大致反映y与x的函数关系的图象是( )| A. | 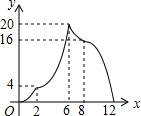 | B. | 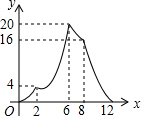 | C. | 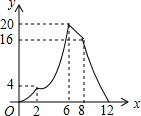 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com