
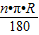 (n为圆心角,R为半径);也考查了旋转的性质.
(n为圆心角,R为半径);也考查了旋转的性质. 

科目:初中数学 来源: 题型:
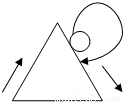
 已知一正三角形的边长是和它相切的圆的周长的两倍,当这个圆按箭头方向从某一位置沿正三角形的三边做无滑动的旋转,直至回到原出发位置时,则这个圆共转了( )
已知一正三角形的边长是和它相切的圆的周长的两倍,当这个圆按箭头方向从某一位置沿正三角形的三边做无滑动的旋转,直至回到原出发位置时,则这个圆共转了( )查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 已知一正三角形的边长是和它相切的圆的周长的两倍,当这个圆按箭头方向从某一位置沿正三角形的三边做无滑动的旋转,直至回到原出发位置时,则这个圆共转了
已知一正三角形的边长是和它相切的圆的周长的两倍,当这个圆按箭头方向从某一位置沿正三角形的三边做无滑动的旋转,直至回到原出发位置时,则这个圆共转了查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:
已知正方形ABCD的边长AB=k(k为正整数)正三角形PAE的顶点P在正方形内,顶点E在边AB上,且AE=1,将△PAE在正方形内按图1中所示的方式,沿着正方形的边AB、BC、CD、DA、AB……连续地翻转n次,使顶点P第一次回到原来的起始位置.


(1) (2)
(1)如果我们把正方形ABCD的边展开在一直线上,那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动,图2是k=1时,△PAE沿正方形的边连续翻转过程的展开示意图.请你探究:若k=1,则△PAE沿正方形的边连续翻转的次数n=________时,顶点P第一次回到原来的起始位置.
(2)若k=2,则n=______时,顶点P第一次回到原来的起始位置;若k=3,则n=____时,顶点P第一次回到原来的起始位置.
(3)请你猜测:使顶点P第一次回到原来起始位置的n值与k之间的关系(请用含k的代数式表示n).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com