
如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC-CB=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
(1)7;(2)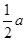 ;(3)
;(3)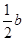 .
.
解析试题分析:(1)据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可.
(2)据题意画出图形即可得出答案.
(3)据题意画出图形即可得出答案.
试题解析:(1)如图
∵AC=8cm,CB=6cm,∴AB=AC+CB=8+6=14cm,又∵点M、N分别是AC、BC的中点,∴MC=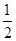 AC,CN=
AC,CN=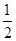 BC,∴MN=
BC,∴MN=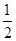 AC+
AC+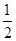 BC=
BC=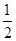 ( AC+BC)=
( AC+BC)=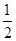 AB=7cm.
AB=7cm.
答:MN的长为7cm.
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,则MN=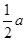 cm,
cm,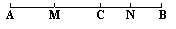
理由是:∵点M、N分别是AC、BC的中点,∴MC=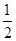 AC,CN=
AC,CN=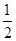 BC,∵AC+CB=acm,MN=
BC,∵AC+CB=acm,MN=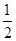 AC+
AC+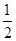 BC=
BC=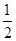 (AC+BC)=
(AC+BC)=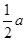 cm.
cm.
(3)解:如图,
∵点M、N分别是AC、BC的中点,∴MC=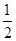 AC,CN=
AC,CN=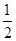 BC,∵AC-CB=bcm,MN=
BC,∵AC-CB=bcm,MN=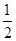 AC-
AC-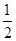 BC=
BC=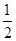 (AC-BC)=
(AC-BC)=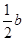 cm.
cm.
考点:两点间的距离.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
如图,EF//AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=80°,
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,将一副三角板,如图放置在桌面上,让三角板OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角板OCD不动,把三角板OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止。
(1)如下图,当三角板OAB转动了20°时,求∠BOD的度数;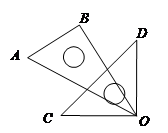
(2)在转动过程中,若∠BOD=20°,在下面两图中分别画出∠AOB的位置,并求出转动了多少度?

(3)在转动过程中,∠AOC与∠BOD有怎样的等量关系,请你给出相等关系式,并说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:单选题
在平行四边形ABCD中,点E在AD上,且AE:ED=3:1,CE的延长线与BA的延长线交于点F,则S△AFE:S四边形ABCE为( )
| A.3:4 | B.4:3 | C.7:9 | D.9:7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com