
分析 (1)根据抛物线的顶点式和顶点坐标(c,b)设解析式,与已知的解析式列等式可求得b和c的值,写出抛物线的解析式;
(2)由A与C的纵坐标相等可得:m和m+6是方程x2+bx+c=n的两根,根据根与系数的关系列方程组可得b和c的值,把B的坐标代入抛物线的解析式中,再把b和c的值代入可得n的值,表示A、B、C三点的坐标,可求△ABC的面积;
(3)先根据(2)和根与系数的关系得:0<3x1+x2<9,0<2x1-b<9,由(2)得:m<x1<m+3,两式相减得b的取值范围.
解答 解:(1)∵抛物线的解析式为:y=x2+bx+c,
∴抛物线解析式中二次顶的系数为1,
设抛物线的解析式为:y=(x-c)2+b,
∴(x-c)2+b=x2+bx+c,
∴$\left\{\begin{array}{l}{-2c=b}\\{{c}^{2}+b=c}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=-6}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为:y=x2-6x+3;
(2)如图1,∵点A(m,n),C(m+6,n)在抛物线y=x2+bx+c上,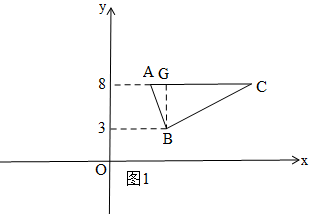
∴m和m+6是方程x2+bx+c=n的两根,
即x2+bx+c-n=0,
∴$\left\{\begin{array}{l}{m+m+6=-b}\\{m(m+6)=c-n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2(m+3)}\\{c={m}^{2}+6m+n}\end{array}\right.$,
∵B(m+1,$\frac{3}{8}$n)在抛物线y=x2+bx+c上,
∴(m+1)2+b(m+1)+c=$\frac{3}{8}$n,
将b、c代入得:(m+1)2-2(m+3)(m+1)+m2+6m+n=$\frac{3}{8}$n,
即n-5=$\frac{3}{8}$n,
n=8,
∴A(m,8),B(m+1,3),C(m+6,8),
∴AC=6,
过B作BG⊥AC于G,则BG=8-3=5,
∴S△ABC=$\frac{1}{2}$×6×5=15;
(3)由题意得:x1+x2=-b,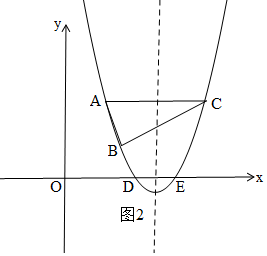
∴x2=-b-x1①,
∵0<x1+$\frac{1}{3}$x2<3,
∴0<3x1+x2<9②,
把①代入②得:0<3x1-b-x1<9,
0<2x1-b<9③,
如图2,A(m,8),C(m+6,8),
∴AC=m+6-m=6,
∴抛物线的对称轴是:x=m+3,
∵x1<x2,
∴m<x1<m+3,
2m<2x1<2m+6④,
④-③得:2m<b<2m-3.
点评 本题考查了抛物线的顶点式、对称点的特点、三角形的面积、二次函数与一元二次方程根与系数的关系、抛物线与x轴的交点,第二问利用抛物线上的点:纵坐标相等的点是对称点,与方程相结合,得到m和m+6是方程x2+bx+c=n的两根是关键,第三问有难度,注意第1问的结论不能应用2、3问.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:填空题
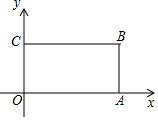 在平面直角坐标系中,A(4,0)、B(4,2)、C(0,2).直线y=kx-k+3(k是常数)将四边形OABC分成面积相等的两部分,则k的值是-2.
在平面直角坐标系中,A(4,0)、B(4,2)、C(0,2).直线y=kx-k+3(k是常数)将四边形OABC分成面积相等的两部分,则k的值是-2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
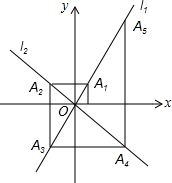 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2007的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2007的坐标为(21008,21009).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
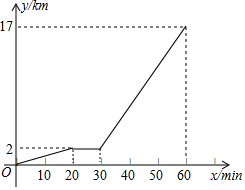 星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:
星期日下午小明去学校,先从家步行到村公所等候同伴,待同伴到齐后一同乘车去学校,下面图象反映了他从家到学校的全过程,图中x轴表示时间,y轴表示小明离家的路程,请根据图象完成下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com