
分析 (1)根据非负数的性质即可得到A点的坐标(2,4),B点的坐标(6,2);
(2)求得直线AB与x轴的交点为D(10,0),于是得到S△ABC=S△ACD-S△BCD,列方程即可得到结论;
(3)根据已知条件列方程即可得到结论.
解答 解:(1)∵(a+b-10)2+|a-b+2|=0,
∴(a+b-10)2=0,|a-b+2|=0,
解得:a=4,b=6,
∴A点的坐标(2,4),B点的坐标(6,2);
(2)∵A点的坐标(2,4),B点的坐标(6,2),
∴直线AB的解析式为:y=-$\frac{1}{2}$x+5,
当y=0时,x=10,
∴直线AB与x轴的交点为D(10,0),
∴S△ABC=S△ACD-S△BCD,
∵点C的坐标为(c,0),
∴$\frac{1}{2}$×(10-c)×4-$\frac{1}{2}$(10-c)×2=10或$\frac{1}{2}$×(c-10)×4-$\frac{1}{2}$(c-10)×2=10
解得:c=0,或c=20,
∴点C的坐标(0,0)或(20,0);
(3)由(2)知,①$\frac{1}{2}$×(10-c)×4-$\frac{1}{2}$(10-c)×2=2或$\frac{1}{2}$×(c-10)×4-$\frac{1}{2}$(c-10)×2=2,
解得:c=8或12,
②$\frac{1}{2}$×(10+c)×4-$\frac{1}{2}$(10+c)×2=12或$\frac{1}{2}$×(|c|-10)×4-$\frac{1}{2}$(c-10)×2=12,
解得:c=-2或c=22,
∴当2≤S△ABC≤12时,则点C的横坐标c的取值范围是-2≤c≤8或12≤c≤22,
故答案为-2≤c≤8或12≤c≤22.
点评 本题考查了坐标与图形旋转,非负数的性质,解方程,三角形的面积的计算,正确的理解题意是解题的关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
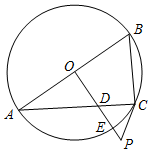 如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com