
【题目】如图,正方形ABCD的边长为1,点E是BC边上一动点(点E不与点B、C重合),以线段DE为边长,作正方形DEFG,使得点F、G落在直线DE的下方,连接AF、BF.当△ABF为等腰三角形时,BE的长为_____.

【答案】![]() 或1-
或1-![]()
【解析】
分两种情形: ①如图1中, 当FA=FB时, 由ΔDCE≌ΔEMF, 推出FM=BM, 推出四边形BMNF是正方形即可解决问题.(2)如图2中,当BA=BF时,根据CE=BM=FN即可解决问题.
解: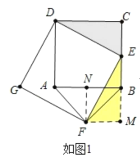
如图1中,当FA=FB时,作FN⊥AB于N,FM⊥CB于M,
![]() 四边形ABCD、DEFG是正方形,
四边形ABCD、DEFG是正方形,
![]() ∠C=∠DEF=∠M=∠ABC=
∠C=∠DEF=∠M=∠ABC=![]() ,DE=EF,DC=BC,
,DE=EF,DC=BC,
![]() ∠DEC+∠FEM=
∠DEC+∠FEM=![]() , ∠CDE+∠DEC=
, ∠CDE+∠DEC=![]() ,
,
![]() ∠CDE=∠FEM ,
∠CDE=∠FEM ,
在ΔDCE和ΔEMF中,
∠C=∠M,∠CDE=∠FEM ,DE=EF
![]() ΔDCE≌ΔEMF,
ΔDCE≌ΔEMF, ![]() FM=CE,CD=EM=BC
FM=CE,CD=EM=BC
![]() BM=EC=FM ,
BM=EC=FM ,
![]() ΔBMF是等腰直角三角形,
ΔBMF是等腰直角三角形,
![]() ∠FBM=∠FBN=
∠FBM=∠FBN=![]() ,
,
![]() ∠FNB=
∠FNB=![]() ,FA=FB,
,FA=FB,
![]() AN=BN=NF=
AN=BN=NF=![]()
![]() ∠M=∠MBN=∠BNF=
∠M=∠MBN=∠BNF=![]() ,
,![]() 四边形BMFN是矩形,
四边形BMFN是矩形,
![]() NF=NB,
NF=NB,
![]() 四边形BMFN 是正方形,
四边形BMFN 是正方形,
![]() BM=FN= CE=EB=
BM=FN= CE=EB=![]()
②如图2中, 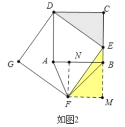
当BA=BF时,由(1)可知,ΔBNF是等腰直角三角形, BF=AB=1,
![]() BM=CE=FN=
BM=CE=FN=![]() ,
,
![]() EB=BC-CE=1-
EB=BC-CE=1-![]()
故答案为![]() 或1-
或1-![]() .
.


科目:初中数学 来源: 题型:
【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
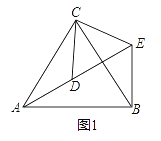
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
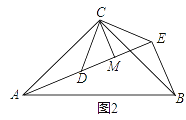
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答下列各题
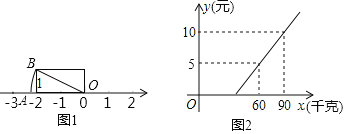
(1)如图1,已知OA=OB,数轴上的点A所表示的数为m,且|m+n|=2
①点A所表示的数m为 ;
②求代数式n2+m﹣9的值.
(2)旅客乘车按规定可以随身携带一定质量的行李,如果超过规定,则需购买行李票,设行李票y(元)是行李质量x(千克)的一次函数,其图象如图2所示.
①当旅客需要购买行李票时,求出y与x之间的函数关系式;
②如果张老师携带了42千克行李,她是否要购买行李票?如果购买需买多少行李票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
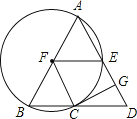
【题目】如图,在![]() 中,
中,![]() ,以AB为直径的
,以AB为直径的![]() 交BD于点C,交AD于点E,
交BD于点C,交AD于点E,![]() 于点G,连接FE,FC.
于点G,连接FE,FC.
![]() 求证:GC是
求证:GC是![]() 的切线;
的切线;
![]() 填空:
填空:
![]() 若
若![]() ,
,![]() ,则
,则![]() 的面积为______.
的面积为______.
![]() 当
当![]() 的度数为______时,四边形EFCD是菱形.
的度数为______时,四边形EFCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
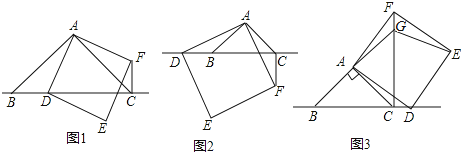
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系,
②BC,CD,CF之间的数量关系为;
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;
若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,求CF,EG.
BC,求CF,EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com