
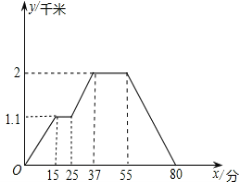
【题目】下图反映的过程是王老师步行从家去书店买书,又去超市买菜, 然后回家.其中x表示时间,y表示王老师离家的距离.根据图象回答下列问题:
(1)书店离王老师家多远?王老师从家到书店用了多少时间?
(2)超市离书店多远?超市离王老师家多远?王老师从超市走回家平均速度是多少?
【答案】(1)1.1千米,15分钟;(2)0.9千米,2千米,80米/分.
【解析】
(1)小明第一个到达的地方应是书店,也应是第一次路程不再增加的开始,所对应的时间为15分,路程为1.1千米.
(2)小明第二个到达的地方应是超市,也应是第二次路程不再增加的开始,所对应的路程为2千米,那么距离超市应是2-1.1(千米):买菜所用时间应是第二次与x轴平行的线段所对应的时间的差:55-37(分钟);超市就是小明到达的最远的地方,平均速度=总路程÷总时间.
解:(1)由图象可以看出书店离小明家1.1千米,小明走到书店用了15分;
(2)超市离书店:2-1.1=0.9(千米),小明在超市用了55-37=18(分);由图象可以看出超市离小明家2千米,小明从书店走回家的平均速度是![]() =80米/分.
=80米/分.
答:(1)书店离王老师家1.1千米,王老师从家到书店用了15分;
(2)超市离书店0.9千米,超市离王老师家2千米,王老师从超市走回家平均速度是80米/分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线相等的四边形叫做和美四边形.
![]() 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子.
![]() 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
![]() 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,![]() ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好治理河流水质,保护环境,某市治污公司决定购买10台污水处理设备,现有A,B两种型号的设备,其中每台的价格,月处理污水量如表:
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 220 | 180 |
经调查:购买一台A型设备比购买一台B型设备多3万元,购买2台A型设备比购买3台B型设备少3万元.
(1)求a,b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过100万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理的污水量不低于1880吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
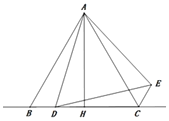
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:BD=CE;
(2)若点D在线段BC上,问点D运动到何处时,AC⊥DE?请说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园计划购进一批甲、乙两种玩具,已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的价格分别是多少元?
(2)该幼儿园计划用3500元购买甲、乙两种玩具,由于采购人员把甲、乙两种玩具的件数互换了,结果需4500元,求该幼儿园原计划购进甲、乙两种玩具各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠A=∠B=70°.请按如下要求操作并解答:

(1)在图中,过点A画直线MP∥BC,过点C画直线NP⊥AB,直线MP与NP交于点P,求∠APC的度数;
(2)在(1)的前提下,直线PM上存在点D,且∠ABD=∠ADB,求直线BD与直线PN相交所形成的锐角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com