Question

6．如图，抛物线y=$\frac{1}{2}$x²+bx+c与直线l：y=kx+m交于A（4，2）、B（0，-1）两点．
（1）求抛物线与直线的解析式；
（2）若点D是直线l下方抛物线上的一动点，过点D作DE∥y轴交直线l于点E，求DE的最大值，并求出此时D的坐标；
（3）在（2）的条件下，DE取最大值时，点P在直线AB上，平面内是否存在点Q，使得以点D、E、P、Q为顶点的四边形为菱形？若存在，直接写出Q点坐标；若不存在，请说明理由．

Answer 1

分析 （1）由抛物线y=$\frac{1}{2}$x²+bx+c与直线l：y=kx+m交于A（4，2）、B（0，-1）两点，直接利用待定系数法求即即可求得答案；
（2）首先设点D的坐标为：（x，$\frac{1}{2}$x²-$\frac{5}{4}$x-1），则点E的坐标为：（x，$\frac{3}{4}$x-1），则可得ED=（$\frac{3}{4}$x-1）-（$\frac{1}{2}$x²-$\frac{5}{4}$x-1），继而求得答案；
（3）分别从4方面去分析求解，注意根据题意画出图形，结合图形求解即可求得答案．

解答 解：（1）∵抛物线y=$\frac{1}{2}$x²+bx+c与直线l：y=kx+m交于A（4，2）、B（0，-1）两点，
∴$\left\{\begin{array}{l}{\frac{1}{2}×{4}^{2}+4b+c=2}\\{c=-1}\end{array}\right.$，$\left\{\begin{array}{l}{4k+m=2}\\{m=-1}\end{array}\right.$，λ
解得：$\left\{\begin{array}{l}{b=-\frac{5}{4}}\\{c=-1}\end{array}\right.$，$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{m=-1}\end{array}\right.$．
∴抛物线的解析式为：y=$\frac{1}{2}$x²-$\frac{5}{4}$x-1，直线的解析式为：y=$\frac{3}{4}$x-1；

（2）设点D的坐标为：（x，$\frac{1}{2}$x²-$\frac{5}{4}$x-1），则点E的坐标为：（x，$\frac{3}{4}$x-1），
∴ED=（$\frac{3}{4}$x-1）-（$\frac{1}{2}$x²-$\frac{5}{4}$x-1）=-$\frac{1}{2}$x²+2x=-$\frac{1}{2}$（x-2）²+2，
∴DE的最大值为：2，
∴此时D的坐标为：（2，-$\frac{3}{2}$）；

（3）当DE取最大值时，E的坐标为：（2，$\frac{1}{2}$），
∴DE=2，
①如图1，PE=PQ=DE=2，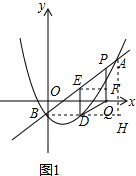
过点E作EF⊥PQ于点F，过点Q作AH⊥x轴，过点B作BH⊥y轴，交于点H，
则△PEF∽△ABH，
∴$\frac{EF}{BH}=\frac{PE}{AB}$，
∵A（4，2）、B（0，-1），
∴BH=4，AH=3，
∴OA=$\sqrt{B{H}^{2}+A{H}^{2}}$=5，
∴$\frac{EF}{4}=\frac{2}{5}$，
∴EF=$\frac{8}{5}$，
∴点P与点Q的横坐标为：2+$\frac{8}{5}$=$\frac{18}{5}$，
∴点P的纵坐标为：$\frac{3}{4}$×$\frac{18}{5}$-1=$\frac{17}{10}$，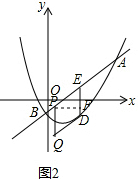
∴点Q的纵坐标为：$\frac{17}{10}$-2=-$\frac{3}{10}$，
∴点Q的坐标为：（$\frac{18}{5}$，-$\frac{3}{10}$）；
②如图2，此时四边形过点P作PF⊥DE于点F，
由①得：PF=$\frac{8}{5}$，
∴点P与点Q的横坐标为：2-$\frac{8}{5}$=$\frac{2}{5}$，
∴点P的纵坐标为：$\frac{3}{4}$×$\frac{2}{5}$-1=-$\frac{7}{10}$，
∴点Q的纵坐标为：-$\frac{7}{10}$-2=-$\frac{27}{10}$，
∴点Q的坐标为：（$\frac{2}{5}$，-$\frac{27}{10}$）；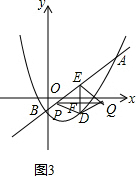
③如图3，作DE的垂直平分线，垂足为F，交直线AB于点P，则PF=QF，
此时点P的纵坐标为：-$\frac{1}{2}$，
∴-$\frac{1}{2}$=$\frac{3}{4}$x-1，
解得：x=$\frac{2}{3}$，
∴PF=2-$\frac{2}{3}$=$\frac{4}{3}$，
∴PQ=2PF=$\frac{8}{3}$，
∴点Q的横坐标为：$\frac{2}{3}$+$\frac{8}{3}$=$\frac{10}{3}$，
∴点Q的坐标为：（$\frac{10}{3}$，-$\frac{1}{2}$）；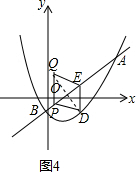
④如图4，过点D作DF⊥AB于点F，则当PF=EF，
由①易得：EF=$\frac{6}{5}$，则EP=$\frac{12}{5}$，
∴点P的纵坐标为：$\frac{1}{2}$-$\frac{12}{5}$×$\frac{3}{5}$=-$\frac{47}{50}$，
∴点P的横坐标为：-$\frac{47}{50}$=$\frac{3}{4}$x-1，
解得：x=$\frac{6}{75}$，
∴点Q的坐标为：（$\frac{6}{75}$，-$\frac{47}{50}$+2），即（$\frac{6}{75}$，$\frac{53}{50}$）；
综上所述：点Q的坐标为：（$\frac{18}{5}$，-$\frac{3}{10}$），（$\frac{2}{5}$，-$\frac{27}{10}$），（$\frac{10}{3}$，-$\frac{1}{2}$），（$\frac{6}{75}$，$\frac{53}{50}$）．

点评 此题属于二次函数的综合题，考查了待定系数求函数解析式、二次函数的最值以及相似三角形的判定与性质．注意掌握分类讨论思想的应用是解此题的关键．