
如图,已知AB为![]() O的直径,AC为弦,CD⊥AB于D,若AE=AC,BE交
O的直径,AC为弦,CD⊥AB于D,若AE=AC,BE交![]() O于点F,连结CF、DE.求证:
O于点F,连结CF、DE.求证:

(1)AE2=AD·AB;
(2)∠ACF=∠AED.
|
解答:(1)连结BC,因为在 ∴∠ACB= 又CD⊥AB于D ∴△ACD∽△ABC ∴ 则AC2=AD·AB 又AC=AE ∴AE2=AD·AB. (2)∵AE2=AD·AB ∴ 又∠EAD=∠BAE ∴△EAD∽△BAE ∴∠AED=∠ABE 又∵∠ABE=∠ACF ∴∠AED=∠ACP. 评析:遇到直径,一般可考虑作出直径所对的圆周角.得到直角三角形,这是一种常用方法. |
|
思路与技巧:连结BC,由AB是 |


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
 16、如图,已知AB为⊙O的弦,M为AB的中点,P为⊙O上任意一点,以点P为圆心、2MO为半径作圆并交⊙O于点C、D,AC、BD交于点Q,请问:
16、如图,已知AB为⊙O的弦,M为AB的中点,P为⊙O上任意一点,以点P为圆心、2MO为半径作圆并交⊙O于点C、D,AC、BD交于点Q,请问:查看答案和解析>>
科目:初中数学 来源: 题型:
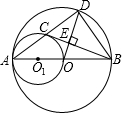 如图,已知AB为⊙O的直径,⊙O1以OA为直径,⊙O的弦AD交⊙O1于点C,BC⊥OD于点E.
如图,已知AB为⊙O的直径,⊙O1以OA为直径,⊙O的弦AD交⊙O1于点C,BC⊥OD于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com