
【题目】已知,A点的坐标为(4,3),过A点分别作坐标轴的垂线,交x轴和y轴分别于B点和C点,P为线段AB上一个动点(P不与A,B重合),过点P的反比例函数y= ![]() 的图象与AC交于点D.
的图象与AC交于点D.

(1)当△PBC的面积等于4时,求该反比例函数的解析式;
(2)当k为何值时,△PBD的面积最大,最大面积是多少?
【答案】
(1)
解:∵A点的坐标为(4,3),
∴P点的横坐标为4,
∵△PBC的面积等于4,
∴PB=2,
∴P(4,2),
∴k=2×4=8,
∴反比例函数的解析式为:y= ![]() ;
;
(2)
解:设D( ![]() ,3),P(4,
,3),P(4, ![]() ),
),
∴S△PBD= ![]() PBAD=
PBAD= ![]() ×
× ![]() ×(4﹣
×(4﹣ ![]() )=﹣
)=﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() (k﹣6)2+
(k﹣6)2+ ![]() ,
,
∴当k=6时,△PBD的面积最大,最大面积是 ![]() .
.
【解析】(1)根据已知条件得到P点的横坐标为4,由△PBC的面积等于4,得到P(4,2),于是得到结论;(2)设D( ![]() ,3),P(4,
,3),P(4, ![]() ),根据三角形的面积公式得到二次函数的解析式,求出二次函数的最值即可.
),根据三角形的面积公式得到二次函数的解析式,求出二次函数的最值即可.
【考点精析】根据题目的已知条件,利用比例系数k的几何意义和二次函数的最值的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


科目:初中数学 来源: 题型:
【题目】感知:如图①,点E在正方形ABCD的边BC上,BF⊥AE于点F,DG⊥AE于点G,可知△ADG≌△BAF.(不要求证明)
拓展:如图②,点B、C分别在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC,求证:△ABE≌△CAF.
应用:如图③,在等腰三角形ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为9,则△ABE与△CDF的面积之和为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图1).数学兴趣小组的小亮同学在塔上观景点P处,利用测角仪测得运河两岸上的A,B两点的俯角分别为17.9°,22°,并测得塔底点C到点B的距离为142米(A、B、C在同一直线上,如图2),求运河两岸上的A、B两点的距离(精确到1米).
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin17.9°≈0.31,cos17.9°≈0.95,tan17.9°≈0.32) 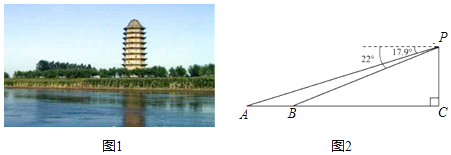
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动: ①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元一律打九折;
③一次性购书超过200元一律打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC与BC相交于点D,若BD=4,CD=2,则AC的长是( )
A.4
B.3
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC与点G,连结AG、CF.则S△FCG为( ) 
A.3.6
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自开展“学生每天锻炼1小时”活动后,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题: 
(1)该校本次调查中,共调查了多少名学生?
(2)请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.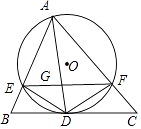
(1)求证:BC是⊙O的切线;
(2)若已知AE=12,CF=6,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com