
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3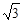 ,AE=3,求AF的长.
,AE=3,求AF的长.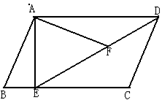
(1)证明见解析;(2)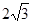 .
.
解析试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在在Rt△ADE中,利用勾股定理求出线段AE的长度.
试题解析:(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180°
∵∠AFE+∠AFD=180 ∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4
又∵AE⊥BC
∴ AE⊥AD
在Rt△ADE中,DE=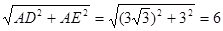
∵△ADF∽△DEC
∴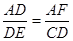
∴
AF=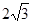
考点:1.相似三角形的判定与性质;2.勾股定理;3.平行四边形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:计算题
(1)如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE//BC,AQ交DE于点P,求证:
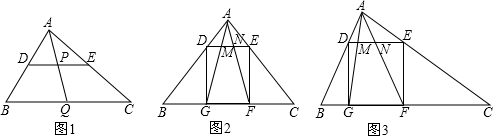
(2)如图,△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG,AF分别交DE于M,N两点.
①如图2,若AB=AC=1,直接写出MN的长;
②如图3,求证:MN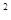 =DM·EN
=DM·EN
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
(1)将矩形各顶点的横、纵坐标都乘以2,写出各对应点A1B1C1D1的坐标;顺次连接A1B1C1D1,画出相应的图形.
(2)求矩形A1B1C1D1与矩形ABCD的面积的比 _________ .
(3)将矩形ABCD的各顶点的横、纵坐标都扩大n倍(n为正整数),得到矩形AnBnCnDn,则矩形AnBnCnDn与矩形ABCD的面积的比为 _________ .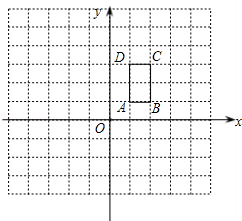
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
课本作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法。
我们有多种剪法,图1是其中的一种方法:
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线。
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=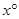 ,试画出示意图,并求出
,试画出示意图,并求出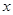 所有可能的值;
所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B,请画出△ABC的三分线,并求出三分线的长。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
(1)求证:DE与⊙O 相切.
(2)若tanC=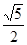 ,DE=2,求AD的长.
,DE=2,求AD的长.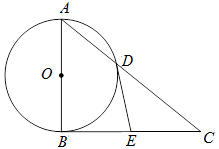
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com