Question

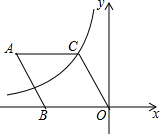
18．如图，在菱形ABOC中，∠A=60°，它的一个顶点C在反比例函数y=$\frac{k}{x}$的图象上，若将菱形向下平移2个单位，点A恰好落在函数图象上，则反比例函数解析式为（　　）

• A． y=-$\frac{{3\sqrt{3}}}{x}$
• B． y=-$\frac{{\sqrt{3}}}{x}$
• C． y=-$\frac{3}{x}$
• D． y=$\frac{{\sqrt{3}}}{x}$

Answer 1

分析 过点C作CD⊥x轴于D，设菱形的边长为a，根据菱形的性质和三角函数分别表示出C，以及点A向下平移2个单位的点，再根据反比例函数图象上点的坐标特征得到方程组求解即可．

解答 解：过点C作CD⊥x轴于D，
设菱形的边长为a，
在Rt△CDO中，OD=a•cos60°=$\frac{1}{2}$a，CD=a•sin60°=$\frac{\sqrt{3}}{2}$a，
则C（-$\frac{1}{2}$a，$\frac{\sqrt{3}}{2}$a），
点A向下平移2个单位的点为（-$\frac{1}{2}$a-a，$\frac{\sqrt{3}}{2}$a-2），即（-$\frac{3}{2}$a，$\frac{\sqrt{3}}{2}$a-2），
则$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}a=\frac{k}{-\frac{1}{2}a}}\\{\frac{\sqrt{3}}{2}a-2=\frac{k}{-\frac{3}{2}a}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=2\sqrt{3}}\\{k=-3\sqrt{3}}\end{array}\right.$．
故反比例函数解析式为y=-$\frac{{3\sqrt{3}}}{x}$．
故选：A．

点评 本题考查的是反比例函数综合题目，考查了反比例函数解析式的求法、坐标与图形性质、菱形的性质、平移的性质等知识；本题综合性强，有一定难度．