
【题目】在正方形![]() 中,
中,![]() ,对角线交于点
,对角线交于点![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针转
逆时针转![]() ,交
,交![]() 于点
于点![]() , 则
, 则![]() 的长为____________.
的长为____________.
【答案】![]() 或
或![]()
【解析】
根据正方形的性质得到AC=6![]() ,AC⊥BD,求得AO=BO=
,AC⊥BD,求得AO=BO=![]() ,CP=4
,CP=4![]() ,根据勾股定理得到PB=
,根据勾股定理得到PB=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
解:如图1,
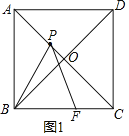
在正方形ABCD中,AB=6,
∴AC=6![]() ,AC⊥BD,
,AC⊥BD,
∴AO=BO=![]() AC=3
AC=3![]() ,
,
∵OP=![]() ,
,
∴CP=4![]() ,
,
在Rt△BPO中,PB=![]() ,
,
∵∠BPF=∠BAP=∠PCF=45°,
∴∠APB=∠PFC=135°-∠FPC,
∴△APB∽△CFP,
∴![]() ,即
,即![]() ,
,
∴PF=![]() ,
,
如图2,
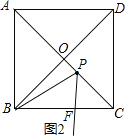
在正方形ABCD中,AB=6,
∴AC=6![]() ,AC⊥BD,
,AC⊥BD,
∴AO=BO=![]() AC=3
AC=3![]() ,
,
∵OP=![]() ,
,
∴CP=2![]() ,
,
在Rt△BPO中,PB=![]() ,
,
∵∠BPF=∠BAP=∠PCF=45°,
∴∠APB=∠PFC=135°-∠FPC,
∴△APB∽△CFP,
∴![]() ,即
,即![]() ,
,
∴PF=![]() ,
,
综上所述:PF的长为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】若一个函数的解析式等于另两个函数解析式的和,则这个函数称为另两个函数的“生成函数”。现有关于x的两个二次函数y1、y2,且y1=a(x-m)2+4(m>0),y1、y2的“生成函数”为:y=x2+4x+14;当x=m时,y2=15;二次函数y2的图象的顶点坐标为(2,k)。
(1)求m的值;
(2)求二次函数y1、y2的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面![]() 时,水面宽
时,水面宽![]() 为
为![]() .当水面上升
.当水面上升![]() 时达到警戒水位,此时拱桥内的水面宽度是多少
时达到警戒水位,此时拱桥内的水面宽度是多少![]() ?
?
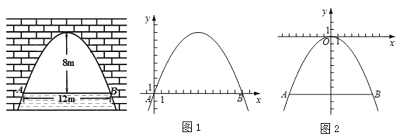
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1.以点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,此时点
,此时点![]() 的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当
的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当![]() 时,求出此时自变量
时,求出此时自变量![]() 的取值,即可解决这个问题.
的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为![]() 轴.建立平面直角坐标系
轴.建立平面直角坐标系![]() ,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即
,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即![]() _______时,求出此时自变量
_______时,求出此时自变量![]() 的取值为_______,从而得水面宽为
的取值为_______,从而得水面宽为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在条直线上的三点![]() 为楼底),
为楼底),![]() ,她在
,她在![]() 处测得广告牌顶端
处测得广告牌顶端![]() 的仰角为
的仰角为![]() ,在
,在![]() 处测得商场大楼楼顶
处测得商场大楼楼顶![]() 的仰角为
的仰角为![]()
![]() 米.已知广告牌的高度
米.已知广告牌的高度![]() 米,求这座商场大楼的高度
米,求这座商场大楼的高度![]() (
(![]() ,小红的身高不计,结果保留整数).
,小红的身高不计,结果保留整数).
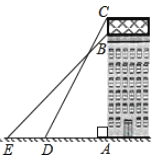
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、 点
、 点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 上,
上, ![]() 平分
平分![]() .
.
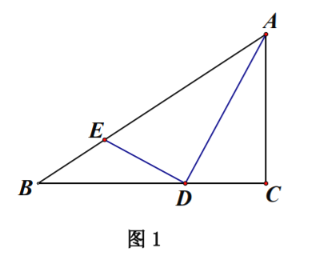
![]() 如图1,求证:
如图1,求证:![]() .
.
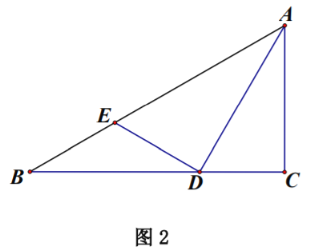
![]() 如图2,若
如图2,若![]() .求证:
.求证:![]() .
.
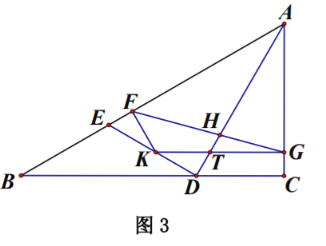
![]() 在
在![]() 问的条件下,如图3, 在线段
问的条件下,如图3, 在线段![]() 上取一点
上取一点![]() ,使
,使![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1),(2)两题
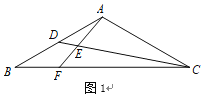
数学课上,老师出示了这样一道题:如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点,且满足
上一点,且满足![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.同学们经过思考后,交流了自己的想法:
的值.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过构造全等三角形,经过进一步推理,就可以求出![]() 的值.”
的值.”
……
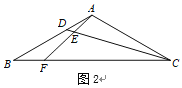
老师:“把原题条件中的‘![]() ’,改为‘
’,改为‘![]() ’其他条件不变(如图2),也可以求出
’其他条件不变(如图2),也可以求出![]() 的值.
的值.
(1)在图1中,①求证:![]() ;②求出
;②求出![]() 的值;
的值;
(2)如图2,若![]() ,直接写出
,直接写出![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数 y=f(x)满足:对于自变量 x 的取值范围内的任意 x1,x2,
(1)若 x1<x2,都有 f(x1)<f(x2),则称 f(x)是增函数;
(2)若 x1<x2,都有 f(x1)>f(x2),则称 f(x)是减函数.
例题:证明函数f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
证明:设 0<x1<x2,
f(x1)﹣f(x2)=![]() .
.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴![]() >0.即 f(x1)﹣f(x2)>0.
>0.即 f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数 f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数![]() .
.
f(﹣1)=![]() +(﹣2)=-1,f(﹣2)=
+(﹣2)=-1,f(﹣2)=![]() +(﹣4)=
+(﹣4)=![]() .
.
(1)计算:f(﹣3)= ,f(﹣4)= ;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
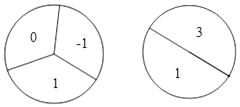
【题目】小明做游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指数字都为x2﹣4x+3=0的根时,他就可以获得一次为大家表演节目的机会.
(1)利用树状图或列表的方法(只选一种)表示出游戏可能出现的所有结果;
(2)求小明参加一次游戏就为大家表演节目的机会的概率是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com