
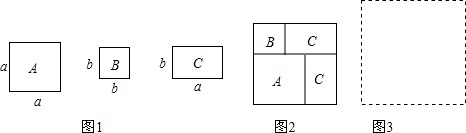
分析 (1)利用面积相等易得a2+2ab+b2=(a+b)2;
(2)由于有a2+3ab,则a2+3ab+nb2分解为(a+b)(a+2b),因此得到n=2,再画图;
(3)利用面积可分解因式.
解答 解:(1)利用面积相等得a2+2ab+b2=(a+b)2;
(2)由于有a2+3ab,则a2+3ab+nb2分解为(a+b)(a+2b),因此得到n=2,
如图:
(3)a2+5ab+4b2=(a+b)(a+4b).
故答案为a2+2ab+b2=(a+b)2;2;a2+5ab+4b2=(a+b)(a+4b).
点评 本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
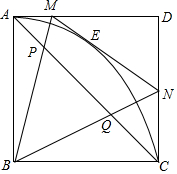 已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.
已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
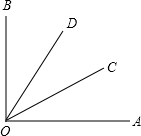 如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.
如图,∠AOC=∠COD=∠BOD,则OD平分∠BOC,OC平分∠AOD,∠AOB=$\frac{3}{2}$∠ADC=$\frac{3}{2}$∠BOC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com