
【题目】如图,点A、B、C、P在⊙O上,CD⊥OA,CE⊥OB,垂足分别为D,E,∠DCE=40°,则∠P的度数为( )

A.70°B.60°C.40°D.35°
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】受疫情的影响,很多农产品滞销,各大电商发起了“爱心助农”活动,帮助农户进行农产品销售.已知某种橘子的成本为4元/千克,经过市场调查发现,一天内橘子的销售量y(千克)与销售单价x(元/千克)(4≤x≤10)的函数关系如下图所示:

(1)当4≤x≤8时,求y与x的函数解析式;
(2)当4≤x≤8时,要使一天内获得的利润为1200元,单价应定为多少?
(3)求橘子的单价定为多少时,一天内获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数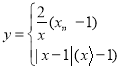 的图象与性质.列表:
的图象与性质.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示.
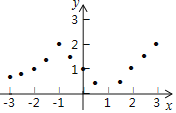
(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象;
(2)研究函数并结合图象与表格,回答下列问题:
①点![]() ,
,![]() ,
,![]() ,
,![]() 在函数图象上,
在函数图象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②当函数值![]() 时,求自变量x的值;
时,求自变量x的值;
③在直线![]() 的右侧的函数图象上有两个不同的点
的右侧的函数图象上有两个不同的点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直线![]() 与函数图象有三个不同的交点,求a的取值范围.
与函数图象有三个不同的交点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如下图:
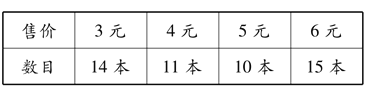
下列说法正确的是( )
A.该班级所售图书的总数收入是226元
B.在该班级所售图书价格组成的一组数据中,中位数是4
C.在该班级所售图书价格组成的一组数据中,众数是15
D.在该班级所售图书价格组成的一组数据中,方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车同时从A地出发,匀速开往B地,甲车行驶到B地后立即沿原路线以原速度返回A地,到达A地后停止运动:当甲车到达A地时,乙车恰好到达B地,并停止运动.已知甲车的速度为150km/h,设甲车出发xh后,甲、乙两车之间的距离为ykm,图中的折线OMNQ表示了整个运动过程中y与x之间的函数关系.

(1)A、B两地的距离是 km,乙车的速度是 km/h;
(2)指出点M的实际意义,并求线段MN所表示的y与x之间的函数表达式;
(3)当两车相距50km时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
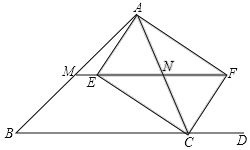
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
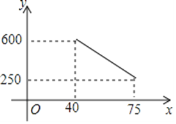
【题目】据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为![]() (元),求每月获得利润
(元),求每月获得利润![]() (元)关于销售单价
(元)关于销售单价![]() (元)的函数解析式;
(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com