
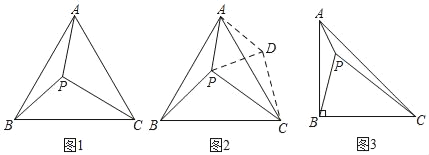
【题目】(1)如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内,如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴ =AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°
∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4, =∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC= °
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
(2)如图3,在△ABC中,AB=BC,∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.
【答案】(1)PD,∠CAD,∠APB,90;(2)135°.
【解析】
(1)如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.只要证明△ABP≌△ACD(SAS),推出BP=CD=4,∠APB=∠ADC,再利用勾股定理的逆定理即可解决问题;
(2)把△PAC绕A点逆时针旋转90°得到△DBA,如图,想办法证明△BPD是等腰三角形即可解决问题;
(1)如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴PD=AD=AP=3,∠ADP=∠PAD=60°,
∵△ABC是等边三角形,
∴AC=AB,∠BAC=60°,
∴∠BAP=∠CAD,
∴△ABP≌△ACD(SAS),
∴BP=CD=4,∠APB=∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC=90°
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
故答案为:PD,∠CAD,∠APB,90.
(2)解:∵∠ABC=90°,BC=AB,
∴把△PAC绕A点逆时针旋转90°得到△DBA,如图,
∴BD=PC=3,AD=AP=2,∠PAD=90°,
∴△PAD为等腰直角三角形,
∴DP=![]() PA=2
PA=2![]() ,∠DPA=45°,
,∠DPA=45°,
在△BPD中,PB=2,PD=2![]() ,DB=3,
,DB=3,
∵12+(2![]() )2=32,
)2=32,
∴AP2+PD2=BD2,
∴△BPD为直角三角形,
∴∠BPD=90°,
∴∠APB=∠APD+∠DPB=90°+45°=135°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;
(3)结合函数的图象,写出该函数的一条性质:_____________________________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是___________________.
有2个实数根,则t的取值范围是___________________.
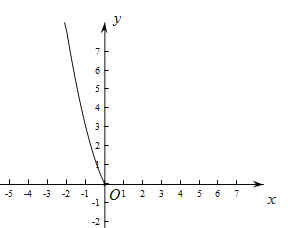
查看答案和解析>>
科目:初中数学 来源: 题型:
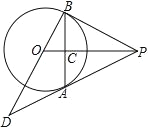
【题目】如图,PA 为⊙O 的切线,A 为切点,过 A 作弦 AB⊥OP,垂足为点 C,延长BO 与 PA 的延长线交于点 D
(1) 求证:PB 为⊙O 的切线
(2) 若 OB=3,OD=5,求 PB 的长
查看答案和解析>>
科目:初中数学 来源: 题型:
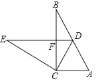
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按逆时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,
(1)求n的值;
(2)若AC=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
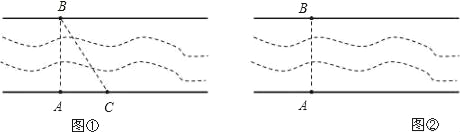
【题目】经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
(1)求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
(2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.(不用考虑计算问题,叙述清楚即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
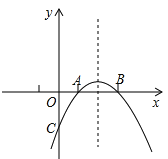
【题目】已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
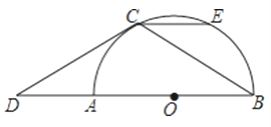
【题目】如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
(1)求∠D的度数;
(2)求证:以点C,O,B,E为顶点的四边形是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com