
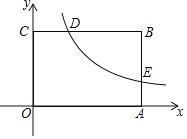
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���A��x����������ϣ�����C��y����������ϣ�D��BC���ϵ�һ�㣬OC��CD��5��3��DB��6������������y��![]() ��k��0���ڵ�һ�����ڵ�ͼ����D����AB�ڵ�E��AE��BE��1��2��
��k��0���ڵ�һ�����ڵ�ͼ����D����AB�ڵ�E��AE��BE��1��2��
��1������������������ı���ʽ��
��2������P�ھ���OABC�ڣ�������S��PAO��![]() S�ı���OABC��
S�ı���OABC��
������P�����������������ͼ���ϣ����P�����ꣻ
������Q��ƽ����һ��ʹ����A��B��P��QΪ������ı������������Q�����꣮
���𰸡���1��y��![]() ����2���٣�
����2���٣�![]() ��4�����ڣ�6��9����9��2
��4�����ڣ�6��9����9��2![]() ����1����
����1����
��������
��1�����B������Ϊ��m��n�������E������Ϊ��m��![]() n������D������Ϊ��m��6��n�������÷���������ͼ���ϵĵ���������������m��ֵ��֮���һ�����n��ֵ��Ȼ���һ����⼴�ɣ�
n������D������Ϊ��m��6��n�������÷���������ͼ���ϵĵ���������������m��ֵ��֮���һ�����n��ֵ��Ȼ���һ����⼴�ɣ�
��2�����������ε������ʽ����ε������ʽ���S��PAO��![]() S�ı���OABC���ɽ�һ�����P��������.������P�����������������ͼ���ϣ����÷���������ͼ���ϵ�����������������P�����ꣻ���ɵ�A��B�����꼰��P��������ɵó�AP��BP�������ɵó�AB����Ϊ�Խ��ߣ����P������Ϊ��t��4������AP��AB��BP��AB����������ǣ���i����AB��APʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P1�����꣬���P1Q1�ij��������Q1�����ꣻ��ii����BP��ABʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P2�����꣬���P2Q2�ij��������Q2�����꣮
S�ı���OABC���ɽ�һ�����P��������.������P�����������������ͼ���ϣ����÷���������ͼ���ϵ�����������������P�����ꣻ���ɵ�A��B�����꼰��P��������ɵó�AP��BP�������ɵó�AB����Ϊ�Խ��ߣ����P������Ϊ��t��4������AP��AB��BP��AB����������ǣ���i����AB��APʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P1�����꣬���P1Q1�ij��������Q1�����ꣻ��ii����BP��ABʱ�����������ľ��빫ʽ�����tֵ�������ɵó���P2�����꣬���P2Q2�ij��������Q2�����꣮
��1�����B��������m��n�������E��������m��![]() n������D��������m��6��n����
n������D��������m��6��n����
�ߵ�D��E�ڷ���������y��![]() ��k��0����ͼ���ϣ�
��k��0����ͼ���ϣ�
��k��![]() mn����m��6��n��
mn����m��6��n��
��m��9��
��OC��CD��5��3��
��n����m��6����5��3��
��n��5��
��k��![]() mn��
mn��![]() ��9��5��15��
��9��5��15��
�෴���������ı���ʽΪy��![]() ��
��
��2����S��PAO��![]() S�ı���OABC��
S�ı���OABC��
��![]() OAyP��
OAyP��![]() OAOC��
OAOC��
��yP��![]() OC��4��
OC��4��
��y��4ʱ��![]() ��4��
��4��
��ã�x��![]() ��
��
������P�����������������ͼ���ϣ���P������Ϊ��![]() ��4����
��4����
���ɣ�1����֪����A������Ϊ��9��0������B������Ϊ��9��5����
��yP��4��yA+yB��5��
��![]() ��
��
��AP��BP��
��AB����Ϊ�Խ��ߣ�
���P��������t��4����
��AP��AB��BP��AB����������ǣ���ͼ��ʾ����

��i����AB��APʱ����9��t��2+��4��0��2��52��
��ã�t1��6��t2��12����ȥ����
���P1��������6��4����
�֡�P1Q1��AB��5��
���Q1��������6��9����
��ii����BP��ABʱ����9��t��2+��5��4��2��52��
��ã�t3��9��2![]() ��t4��9+2
��t4��9+2![]() ����ȥ����
����ȥ����
���P2��������9��2![]() ��4����
��4����
�֡�P2Q2��AB��5��
���Q2��������9��2![]() ����1����
����1����
������������Q��������6��9����9��2![]() ����1����
����1����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����¥![]() ��ǰ����һΧǽ
��ǰ����һΧǽ![]() ���ڵ�
���ڵ�![]() �����¥��
�����¥��![]() ������Ϊ
������Ϊ![]() ����
����![]() �����¥��
�����¥��![]() ������Ϊ
������Ϊ![]() ����
����![]() �ĸ߶�Ϊ2�ף�
�ĸ߶�Ϊ2�ף�![]() ֮��ľ���Ϊ20�ף�
֮��ľ���Ϊ20�ף�![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�.
��ͬһ��ֱ���ϣ�.

��1�������¥![]() �ĸ߶�.
�ĸ߶�.
��2���������![]() ��
��![]() ����֮��ľ���.���ο����ݣ�
����֮��ľ���.���ο����ݣ�![]() ��
��![]() ��
��![]() ���������������
���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
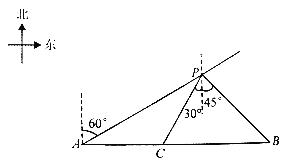
����Ŀ�����գ�������ĸɽ������Ϊ���½����죬��Ϊ�ҹ������ͽ���ĵ�һ�����������ϵĹ�����ĸ������������̫�����Σ���ʹ�ҹ���ΰ����·�ϼ���ǰ����ͼ��ɽ������һ�β����У�Ѳ��������A��ƫ��60�㷽��P���������ں���A����������һ���ɴ�ֻB����BA������ʻ��ɽ�����������ó������ɴ�ֻ��P����ƫ��45�㷽��P��![]() ���ɽ����������P����ƫ��30�㷽��ʻ�����պ���C���ɹ����ؿ��ɴ�ֻ��������ʱ�����ɴ�ֻ�ຣ��A���ж��ٺ����
���ɽ����������P����ƫ��30�㷽��ʻ�����պ���C���ɹ����ؿ��ɴ�ֻ��������ʱ�����ɴ�ֻ�ຣ��A���ж��ٺ����![]() �������ȷ��0.1���
�������ȷ��0.1���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
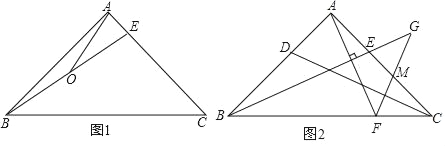
����Ŀ������ABC�У���֪AB=AC����BAC=90�㣬EΪ��AC��һ�㣬����BE��
(1)��ͼ1������ABE=15�㣬OΪBE�е㣬����AO����AO=1����BC�ij���
(2)��ͼ2��DΪAB��һ�㣬������AE=AD������A��AF��BE��BC�ڵ�F������F��FG��CD��BE���ӳ����ڵ�G����AC�ڵ�M����֤��BG=AF+FG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
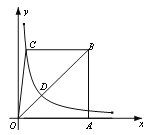
����Ŀ����ͼ����֪����ABCO�ĵױ�AO��![]() ���ϣ�
���ϣ�![]() ��AB��AO������C��˫����
��AB��AO������C��˫����![]() ��OB��D����
��OB��D����![]() ������OBC���������3����k��ֵΪ__________��
������OBC���������3����k��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������A��m+2��3m+4����ֱ��l�ϣ���B��b��0����x���ϣ������BΪԲ�ģ��뾶Ϊ1��Բ��ֱ��l�н��㣬��b��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijС���ſڵ����˴�ˮƽλ��AB�ƹ̶���O��ת��λ��DC����֪����AB�ij�Ϊ3.5�ף�OA�ij�Ϊ3�ף���C��AB�ľ���Ϊ0.3�ף�֧��OE�ĸ�Ϊ0.6�ף���ô���˶˵�D�����ľ���Ϊ____________��
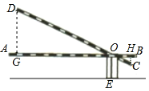
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı�AD��x��ƽ�У�A��B����ĺ�����ֱ�Ϊ1��3������������y��![]() ��ͼ��A��B���㣬������ABCD�������_____��
��ͼ��A��B���㣬������ABCD�������_____��
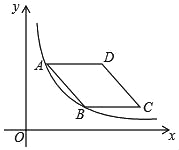
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ���������̨���ԣ��ִ������̳��˽ͬһ���ͺŵĵ��Ա��۾�Ϊ![]() Ԫ�����Ҷ�����һ�����Ż�. ���̳����Ż��������£�
Ԫ�����Ҷ�����һ�����Ż�. ���̳����Ż��������£�
���̳��Ż���������һ̨��ԭ���շѣ������ÿ̨�Ż�![]() ��
��
���̳��Ż�������ÿ̨�Ż�![]() .
.
![]() �蹫˾����
�蹫˾����![]() ̨���ԣ�ѡ����̳�ʱ�� �������Ϊ
̨���ԣ�ѡ����̳�ʱ�� �������Ϊ![]() Ԫ��ѡ�����̳�ʱ���������Ϊ
Ԫ��ѡ�����̳�ʱ���������Ϊ![]() Ԫ����ֱ����
Ԫ����ֱ����![]() ��
��![]() ֮��Ĺ�ϵʽ.
֮��Ĺ�ϵʽ.
![]() ʲô����£������̳����շ���ͬ��ʲô����£������̳�������Żݣ�ʲô����£������̳�������Żݣ�
ʲô����£������̳����շ���ͬ��ʲô����£������̳�������Żݣ�ʲô����£������̳�������Żݣ�
![]() ������Ϊ���裬�ƻ��Ӽ������̳�һ������
������Ϊ���裬�ƻ��Ӽ������̳�һ������![]() ̨ijƷ�Ƶĵ��ԣ����дӼ��̳�����
̨ijƷ�Ƶĵ��ԣ����дӼ��̳�����![]() ̨����.��֪���̳����˷�Ϊÿ̨
̨����.��֪���̳����˷�Ϊÿ̨![]() Ԫ�����̳����˷�Ϊÿ̨
Ԫ�����̳����˷�Ϊÿ̨![]() Ԫ�������˷�Ϊ
Ԫ�������˷�Ϊ![]() Ԫ���ڼ��̳��ĵ��Կ��ֻ��
Ԫ���ڼ��̳��ĵ��Կ��ֻ��![]() ̨������£������������˷����٣������˷��Ƕ��٣�
̨������£������������˷����٣������˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com