
����Ŀ����կ��ѧʳ��Ϊѧ���ṩ�����ּ۸�������ѡ�������ּ۸�ֱ��ǣ�A��3Ԫ��B��4Ԫ��C��5Ԫ��D��6Ԫ��Ϊ���˽�ѧ����������͵Ĺ��������ѧУ������������˼ס�������ѧ��ij�칺��������͵����������ͳ�������Ƴ����µ�ͳ��ͼ����
�ס�������ѧ��������͵����ͳ�Ʊ�
Ʒ�� | A | B | C | D |
�� | 6 | 22 | 16 | 6 |
�� | �� | 13 | 25 | 3 |

��1�����Ұ�ѧ��������
��2�����Ұ����ͷ��õ���λ����
��3����֪�ס����������ͷ��õ�ƽ����Ϊ4.44Ԫ����ƽ�����������ĽǶȽ���ĸ�������ͼ۸�ϸߣ�
��4������ν��ܵ����ѧ���У�������һ�ˣ�ǡ���ǹ���C����͵�ѧ���ĸ����Ƕ��٣�
���𰸡�
��1��
�⣺���Ұ�ѧ������C��͵�����Ϊ25�ˣ�ռ�ٷֱ�Ϊ��50%��
���Ұ�ѧ������Ϊ��25��50%=50���ˣ�
��2��
�⣺���Ұ�ѧ��������50�ˣ�
���Ұ����ͷ��õ���λ��Ӧ��25��26�˵�ƽ������
���Ұ����ͷ��õ���λ���ǣ�����C��ͣ�5Ԫ
��3��
�⣺�ס����������ͷ��õ�ƽ����Ϊ4.44Ԫ���װ����ͷ��õ������ǣ�����B��ͣ�4Ԫ���Ұ����ͷ��õ������ǣ�����C��ͣ�5Ԫ��
���Ұ�����ͼ۸�ϸ�
��4��
�⣺ǡ���ǹ���C����͵�ѧ���ĸ����ǣ� ![]() =
= ![]() ��
��
����������1�����Ұ�ѧ������C��͵�����Ϊ25�ˣ�ռ�ٷֱ�Ϊ��50%����������Ұ�ѧ����������2�����Ұ�ѧ��������50�ˣ���������Ұ����ͷ��õ���λ������3���ɼס����������ͷ��õ�ƽ����Ϊ4.44Ԫ���ɵüװ����ͷ��õ������ǣ�����B��ͣ�4Ԫ���Ұ����ͷ��õ������ǣ�����C��ͣ�5Ԫ��������ô𰸣���4��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
�����㾫����������Ҫ������ͳ�Ʊ�������ͳ��ͼ�����֪ʶ�㣬��Ҫ��������ͳ�Ʊ��IJ��裺��1���ռ��������ݣ���2��ȷ��ͳ�Ʊ��ĸ�ʽ����Ŀ����������ֽ�Ŵ�С�Ƴɱ���3����д��Ŀ������Ŀ���Ƽ����ݣ���4�������ܼƺͺϼƲ�������У�һ���ܼƷ��ں�������ϼƷ����������ϸ�5��д�ñ������Ʋ������Ʊ�ʱ�䣻������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯���������ȷ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����O��EF��AC����AD��E����BC��F������AF��CE�� 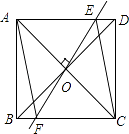
��1����֤���ı���AECF������
��2����AB=3��BC=4��������AECF���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ����С��ACDB����ƽ��ֱ������ϵ�У��õ������������ΪA����6��12����B����6��0����C��0��6����D����6��6�����Ե�BΪ��ת���ģ���ƽ��ֱ������ϵ�ڽ�С��˳ʱ����ת90�㣮 
��1��������ת���С��A��C��D��B�䣻
��2��д����A�䣬C�䣬D������ꣻ
��3������߶�BA��ת��B��A��ʱ��ɨ�������ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڴ���װ��������ͬ��С�����ǵı�ŷֱ�Ϊ2��5���ҿڴ���װ��������ͬ��С�����ǵı�ŷֱ�Ϊ4��9�����ڴ���װ��������ͬ��С�����ǵı�ŷֱ�Ϊ1��6��7������3���ڴ��и����ȡ��һ��С��
��1��������ͼ��ʾ���п��ܳ��ֵĽ����
��2������ȡ��������С��ı�ŷֱ��ʾ�����߶εij�������Щ�߶��ܹ��������εĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬����C����O�����ߣ��е�ΪB������AC����O��D����C=38�㣮��E��AB�Ҳ�İ�Բ���˶�������A��B�غϣ������AED�Ĵ�С�ǣ�������
A.19��
B.38��
C.52��
D.76��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x��ͼ���뺯��y= ![]() ��ͼ���ڵ�һ�����ڽ��ڵ�B����C�Ǻ���y=
��ͼ���ڵ�һ�����ڽ��ڵ�B����C�Ǻ���y= ![]() �ڵ�һ����ͼ���ϵ�һ�����㣬����OBC�����Ϊ3ʱ����C�ĺ������� ��
�ڵ�һ����ͼ���ϵ�һ�����㣬����OBC�����Ϊ3ʱ����C�ĺ������� �� 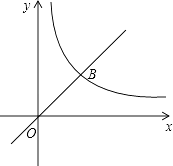
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ߵĶ���Ϊ��0��4������x�ύ�ڣ���2��0������2��0����
��1��ֱ��д�������߽���ʽ��
��2����ͼ��������������ƽ��k����λ����ƽ�ƺ������ߵĶ���ΪD����x��Ľ���ΪA��B����ԭ�����ߵĽ���ΪP��
�ٵ�ֱ��OD����ABΪֱ����Բ������Eʱ�����ʱk��ֵ��
���Ƿ����������kֵ��ʹ�õ�O��P��D����ǡ����ͬһ��ֱ���ϣ������ڣ����kֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD�У�E��CD��һ�㣬F��CB���ӳ����ϣ���DE=BF�� 
��1����֤����ADE�ա�ABF��
��2���ʣ�����ADE˳ʱ����ת���ٶȺ����ABF�غϣ���ת������ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2����A=120�㣬��P��Q��K�ֱ�Ϊ�߶�BC��CD��BD�ϵ�����һ�㣬��PK+QK����СֵΪ�� �� 
A.1
B.![]()
C.2
D.![]() +1
+1
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com