
【题目】已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC, 
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
【答案】
(1)证明:∵BD垂直平分AC,

∴AB=BC,AD=DC,
在△ADB与△CDB中,
 ,
,
∴△ADB≌△CDB(SSS)
∴∠BCD=∠BAD,
∵∠BCD=∠ADF,
∴∠BAD=∠ADF,
∴AB∥FD,
∵BD⊥AC,AF⊥AC,
∴AF∥BD,
∴四边形ABDF是平行四边形
(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴ABDF是菱形,
∴AB=BD=5,
∵AD=6,
设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2,
即52﹣x2=62﹣(5﹣x)2
解得:x= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AC=2AE= ![]()
【解析】(1)先证得△ADB≌△CDB求得∠BCD=∠BAD,从而得到∠ADF=∠BAD,所以AB∥FD,因为BD⊥AC,AF⊥AC,所以AF∥BD,即可证得.(2)先证得平行四边形是菱形,然后根据勾股定理即可求得.
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中结论正确的个数为( )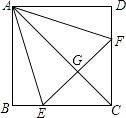
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列叙述中:
①一组对边相等的四边形是平行四边形;
②函数y= ![]() 中,y随x的增大而减小;
中,y随x的增大而减小;
③有一组邻边相等的平行四边形是菱形;
④有不可能事件A发生的概率为0.0001.
正确的叙述有( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( ) 
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于体育选考项目统计图
项目 | 频数 | 频率 |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
合计 | a | 1 |

(1)求出表中a,b,c的值,并将条形统计图补充完整. 表中a= , b= , c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=2.P是AB边上一动点,PD⊥AC于点D,点E在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是( ) 
A.一直减小
B.一直不变
C.先减小后增大
D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月26日,2015黄河口(东营)国际马拉松比赛拉开帷幕,中央电视台体育频道用直升机航拍技术全程直播.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离 米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com