
【题目】如图,AC=AB,DC=DB,AD与BC相交于O. 
(1)求证:△ACD≌△ABD;
(2)求证:AD垂直平分BC.
【答案】
(1)证明:在△ADC和△ADB中,
 ,
,
∴△ACD≌△ABD.
(2)证明:方法一∵△ACD≌△ABD
∴∠BAO=∠CAO
又∵AB=AC,
∴△ABC为等腰三角形,
∴AO⊥BC、CO=BO,
∴AD垂直平分BC.
方法二∵AB=AC,
∴点A在BC的垂直平分线上,
∵DC=DB,
∴点D在BC的垂直平分线上,
∴AD垂直平分BC.

【解析】(1)根据SSS即可证明.(2)根据线段垂直平分线的定义即可证明.
【考点精析】通过灵活运用线段垂直平分线的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是某几何体的三种形状图.
(1)说出这个几何体的名称;
(2)若从正面看到的形状图长为15cm,宽为4cm的长方形,从左面看到的形状图是宽为3cm的长方形,从上面看到的形状图的最长的边长为5cm,求这个几何体的侧面积(不包括上下底面).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE、下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有( ) 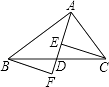
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=![]() 的图象与性质。小慧根据学习函数的经验,对函数y=
的图象与性质。小慧根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
的图象与性质进行了探究。下面是小慧的探究过程,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是__________;
的自变量x的取值范围是__________;
(2)列出y与x的几组对应值。请直接写出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出该函数的两条性质:
①_____________________________________________;
②____________________________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).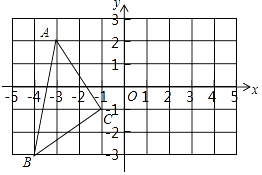
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点C1的坐标(直接写答案):C1;
(3)△A1B1C1的面积为;
(4)在y轴上画出点P,使PB+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.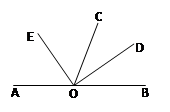
(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过秒钟两人第一次相遇;
若两人同时出发,同向而行,则经过秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com