
分析 依次求出S1、S2、Sn,就发现规律:Sn=$\frac{1}{2}$×$\frac{1}{n(n+1)}$,然后求其和即可求得答案.注意$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
解答 解:∵当n=1时,直线为y=-$\frac{1}{2}$x+$\frac{1}{2}$,
∴直线与两坐标轴的交点为(0,$\frac{1}{2}$),(1,0),
∴S1=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$;
当n=2时,直线为y=-$\frac{2}{3}$x+$\frac{1}{3}$,
∴直线与两坐标轴的交点为(0,$\frac{1}{3}$),($\frac{1}{2}$,0),
∴S2=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{2}$×$\frac{1}{2×(2+1)}$;
当n=3时,直线为y=-$\frac{3}{4}$x+$\frac{1}{4}$,
∴直线与两坐标轴的交点为(0,$\frac{1}{4}$),($\frac{1}{3}$,0),
∴S3=$\frac{1}{2}$×$\frac{1}{3}$×$\frac{1}{4}$=$\frac{1}{2}$×$\frac{1}{3(3+1)}$;
…,
Sn=$\frac{1}{2}$×$\frac{1}{n(n+1)}$,
∴S1+S2+S3+…+S2015=$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$)=$\frac{1}{2}$×(1-$\frac{1}{2016}$)=$\frac{2015}{2×2016}$=$\frac{2015}{4032}$.
故答案为$\frac{2015}{4032}$.
点评 本题考查的是一次函数图象上点的坐标特点,根据题意找出规律是解答此题的关键.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
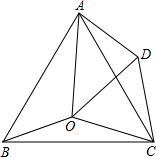 如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.
如图,点O是等边△ABC内一点,以CO为边作等边△COD,∠AOB=110°,∠BOC=α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
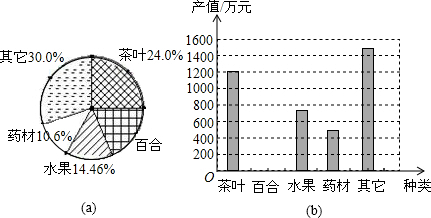
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.
如图,分别以矩形ABCD的顶点A和B为圆心,作半径为1的两个圆正好分别经过C、D两点,若图中两块阴影部分的面积相等,则AB的长度是$\frac{π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com