
 如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形.
如图,已知AB∥CD,∠BAC的平分线与CD交于点E,∠ACD的平分线与AB交于点F,试说明:四边形ACEF是菱形. 科目:初中数学 来源: 题型:解答题
 已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q
已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
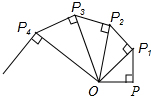 如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.
如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
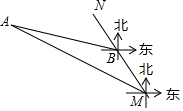 如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)
如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com