
【题目】如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP, 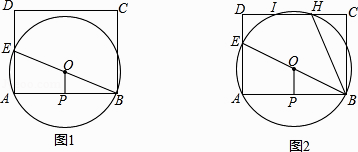
(1)求证:BE是⊙O的直径且OP⊥AB;
(2)若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;
(3)如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.
【答案】
(1)解:∵矩形ABCD,∴∠A=90°,∴BE为直径,
∴OE=OB,
∵AP=BP,
∴OP//AE,AE=2PO,
∴∠OPB=∠A=90°,
即OP⊥AB.
(2)解:此时直线CD与⊙O相切
理由:如图1,延长PO交CD于M,
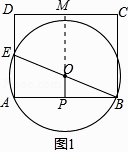
在Rt△ABE中,AB=8,AE=6,
则BE2=62+82=100,
∴BE=10,
∴此时⊙O的半径r=5,∴OM=r=5,
∵在矩形APMD中,PM=AD=8,
∴OM=PM﹣OP=5=r,
∴直线CD与⊙O相切
(3)解:【方法I】如图2,
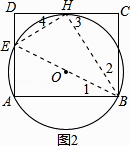
∵BE为直径,
∴∠EHB=90°,
∴∠3+∠4=90°,
∵∠C=90°,
∴∠3+∠2=90°,
∴∠2=∠4,
∴当∠1=∠2时,有
tan∠1=tan∠2=tan∠4,
设AE=x,CH=y,则DE=8﹣x,DH=10﹣y,
∴ ![]() =
= ![]() =
= ![]() ,
,
解得,x=20,或x=5,
∵AE=x<8,∴x=20,不合题意,舍去,取AE=x=5,
Rt△ABE的面积= ![]() AE×AB=
AE×AB= ![]() ×5×10=25.
×5×10=25.
【方法II】如图3,延长PO交CD于点F,连接OH,
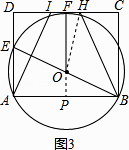
在矩形FPBC,OP⊥AB,且FC=PB= ![]() AB=5,
AB=5,
OP= ![]() AE,OF=8﹣
AE,OF=8﹣ ![]() AE,BE=2HO,
AE,BE=2HO,
当∠ABE=∠CBH时,设tan∠ABE=tan∠CBH=k时,
在Rt△ABE中,则AE=10tan∠ABE=10k,
在Rt△HBC中,则HC=8tan∠ABE=8k,
∴OP=5k,OF=8﹣5k,FH=5﹣8k,
在Rt△ABE中,BE2=AE2+AB2=100(1+k2),
在Rt△OFH中,HO2=FH2+OF2=(5﹣8k)2+(8﹣5k)2,
∵BE=2HO,∴BE2=4 HO2
∴100(1+k2)=4[(5﹣8k)2+(8﹣5k)2],
整理得,2 k2﹣5k+2=0,
解得,k=2,或k= ![]() ,
,
当k=2时,AE=10k=20>8,不合题意,舍去;
当k= ![]() 时,AE=10k=5<8,符合题意,
时,AE=10k=5<8,符合题意,
此时,Rt△ABE的面积= ![]() AE×AB=
AE×AB= ![]() ×5×10=25
×5×10=25
【解析】(1)利用矩形的性质以及平行线分线段成比例定理得出OP//AE,AE=2PO,即可得出答案;(2)首先延长PO交CD于M,求出MO的长等于半径,进而得出答案;(3)根据题意当∠1=∠2时,可得出tan∠1=tan∠2=tan∠4,设AE=x,CH=y,则DE=8﹣x,DH=10﹣y,可得 ![]() =
= ![]() =
= ![]() ,求出x的值,即可得出答案.
,求出x的值,即可得出答案.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ![]() ,则a的值为 .
,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数 ![]() (k为不等于0的常数)的图象在第一象限交于点A(1,n).求:
(k为不等于0的常数)的图象在第一象限交于点A(1,n).求: 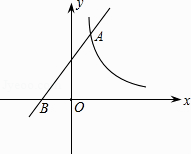
(1)一次函数和反比例函数的解析式;
(2)当1≤x≤6时,反比例函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论: ①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,其中正确的是(填序号).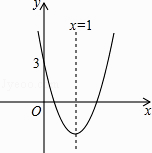
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来. 某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:
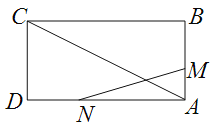
(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时刻t,使以A,M,N为顶点的三角形与![]() 相似?若存在,求t的值;若不存在,请说明理由.
相似?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com