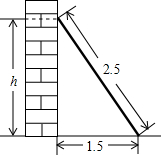
如图.长2.5m的梯子靠在墙上.梯子的底部离墙的底端1.5m.则梯子的顶端与地面的距离为2m．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

4．

如图，长2.5m的梯子靠在墙上，梯子的底部离墙的底端1.5m，则梯子的顶端与地面的距离为2m．

分析直接根据勾股定理即可得出结论．

解答解：∵AC=2.5m，BC=1.5m，
AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{2．{5}^{2}-1．{5}^{2}}$=2（m）．
故答案为：2．

点评本题考查的是勾股定理的应用，熟记勾股定理是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

14．解方程组：$\left\{\begin{array}{l}{2x+y=7}\\{x+2y=8}\end{array}\right.$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．如图，以长方形ABCO中点O为原点，以OC，OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足$\sqrt{a-2b}$+|b-2|=0．
（1）求点A，B和C的坐标．
（2）已知坐标轴上有两动点P，Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动．Q点从O点出发以2个单位长度每秒的速度沿O→A→B→C的路线移动，点Q到达C点整个运动随之结束．若长方形对角线AC，BO的交点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S_△ODP=S_△ODQ？若存在，请求出t的值；若不存在，请说明理由；
（3）点F是线段AC上一点，满足∠FOC=∠FCO，点G是第二象限中一点，连OG，使得∠AOG=∠AOF．点E是线段OA上一动点，连CE交OF于点H，下列两个结论：①$\frac{∠OHC-∠ACE}{∠OEC}$的值不变；②$\frac{∠OHC+∠ACE}{∠OEC}$的值不变，其中有且只有一个结论是正确的，请你找出正确的结论并求其值．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．

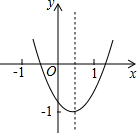如图所示，二次函数y=ax²+bx+c的图象中，王慧同学观察得出了下面四条信息：
（1）b²-4ac＞0；（2）c＞-1；（3）2a+b＜0；（4）a+b+c＜0，其中正确的有（　　）

A．

1个

B．

2个

C．

3个

D．

4个

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

19．要反映某市一周大气中PM2.5的变化情况，宜采用折线统计图．（填“条形”或“折线”或“扇形”）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．

如图，小手盖住的点的坐标可以是（　　）

A．

（5，2）

B．

（3，-4）

C．

（-4，-6）

D．

（-6，3）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

16．某商场将每件进价为20元的玩具以单价为30元的价格出售时，每天可售出300件，经调查当单价每涨1元时，每天少售出10件．若商场想每天获得3750元利润，则每件玩具应涨多少元？这道应用题如果设每件玩具应涨x元，则下列说法错误的是（　　）

	A．	涨价后每件玩具的售价是（30+x）元
	B．	涨价后每天少售出玩具的数量是10x件
	C．	涨价后每天销售玩具的数量是（300-10x）件
	D．	可列方程为（30+x）（300-10x）=3750

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．