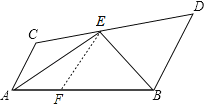
【题目】如图所示，已知AC∥BD，EA，EB分别平分∠CAB和∠DBA，CD过E点．求证：AB＝AC＋BD．
【答案】证明见试题解析．
【解析】
试题分析：在AB上取一点F，使AF=AC，连结EF，就可以得出△ACE≌△AFE，就有∠C=∠AFE．由平行线的性质就有∠C+∠D=180°，由∠AFE+∠EFB=180°得出∠EFB=∠D，在证明△BEF≌△BED就可以得出BF=BD，进而就可以得出结论．
试题解析：证明：在AB上取一点F，使AF=AC，连结EF．
∵EA、EB分别平分∠CAB和∠DBA，∴∠CAE=∠FAE，∠EBF=∠EBD．∵AC∥BD，∴∠C+∠D=180°．在△ACE和△AFE中，∵AC=AF，∠CAE=∠FAE，AE=AE，∴△ACE≌△AFE（SAS），∴∠C=∠AFE．∵∠AFE+∠EFB=180°，∴∠EFB=∠D．在△BEF和△BED中，∵∠EFB=∠D，∠EBF=∠EBD，BE=BE，∴△BEF≌△BED（AAS），∴BF=BD．∵AB=AF+BF，∴AB=AC+BD．
科目：初中数学 来源： 题型：
【题目】如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为( )
A. 
B. 
C. 
D. 不能确定
查看答案和解析>>
科目：初中数学 来源： 题型：
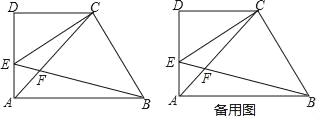
【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设
=y，求y关于x的函数关系式，并写出它的定义域；
（3）当∠ABE的正切值是
时，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝AC，∠BAC＝90°，BD是中线，AF⊥BD，F为垂足，过点C作AB的平行线交AF的延长线于点E.
求证：(1)∠ABD＝∠FAD；(2)AB＝2CE.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把下列各数填入相应的大括号内．
3
，－
，
，0．5，2π，3．14159265，－
，1．103030030003…(相
邻两个3之间依次多1个0)．
(1) 有理数集合：{ }；
(2) 无理数集合：{ }；
(3) 实数集合：{ }；
(4) 负实数集合：{ }．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
