
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
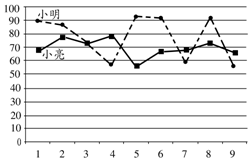 小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
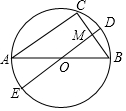 如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于点M.若点E在优弧$\widehat{CAB}$上,AC=8,BC=6,则EM=9.
如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于点M.若点E在优弧$\widehat{CAB}$上,AC=8,BC=6,则EM=9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
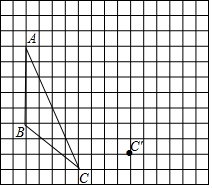 画图并填空,如图:方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′.图中标出了点C的对应点C′.
画图并填空,如图:方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′.图中标出了点C的对应点C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com