
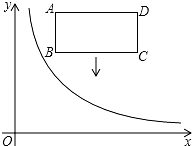
 ��ͼ����ƽ��ֱ������ϵ�У�����������y=$\frac{k}{x}$��x��0����ͼ��;���ABCD�ڵ�һ���ޣ�ADƽ����x�ᣬ��AB=2��AD=4����A������Ϊ��2��6����������ABCD����ƽ�ƣ�ƽ�ƺ�ľ��μ�ΪA��B��C��D����ƽ�ƹ����У�����������ǡ�����ڷ���������ͼ���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�����������y=$\frac{k}{x}$��x��0����ͼ��;���ABCD�ڵ�һ���ޣ�ADƽ����x�ᣬ��AB=2��AD=4����A������Ϊ��2��6����������ABCD����ƽ�ƣ�ƽ�ƺ�ľ��μ�ΪA��B��C��D����ƽ�ƹ����У�����������ǡ�����ڷ���������ͼ���ϣ����� ��1�����ȸ������⣬�����ABCD����ƽ�ƺ��A�������ǣ�2��6-x����C�������ǣ�6��4-x����Ȼ����ݾ���ABCDƽ�ƺ�A�䡢C������ǡ��ͬʱ���ڷ�����������ͼ���ϣ��ɵ�2��6-x��=6��4-x��=k���ݴ����x�������������ƽ�ƺ��A�����꣬���뷴���������Ľ���ʽ���k��ֵ�����������������������ʽ��
��2�����ȷֱ��������E�͵�A���غ�ʱ������F�͵�D���غ�ʱ������ƽ��ʱ����Ƕ��٣�Ȼ��������������1��t��3����3��t��5ʱ���������ۣ����S��t�ĺ�����ϵʽ���ɣ�
��3���������ʱEF��ֱ�߽���ʽ��y=k��x+b�������E�������Ƕ��٣��ٰѵ�E���������EF��ֱ�߽���ʽ���жϳ�k�䡢b�Ĺ�ϵ��Ȼ�����EF��B��B�壬EB���FB�壬���k���ֵ���������b��ֵ��ȷ������ʱEF��ֱ�߽���ʽ���ɣ�
��� �⣺��1���������⣬�ɵ�
B��2��4����C��6��4����D��6��6����
��Ȼ��ƽ�ƺ�A�䡢C������ǡ��ͬʱ���ڷ�����������ͼ���ϣ�
�����ABCD����ƽ�ƾ���Ϊa��
���A�䣨2��6-a������C�䣨6��4-a����
�ߵ�A�䣬C���ڷ���������y=$\frac{k}{x}$��ͼ���ϣ�
��2��6-a��=6��4-a����
���a=3��
�����ƽ�ƺ�A��������ǣ�2��3����
��k=2��6-x��=6��4-x��=k��
�������ɵ�4x=12��
��ã�x=3��
��x=2��y=3���뷴���������Ľ���ʽ��
�ɵã�k=2��3=6��
�෴���������Ľ���ʽ��y=$\frac{6}{x}$��
��2������E�͵�A���غ�ʱ��
��E���������ǣ�y=6��2=3��
����ƽ��ʱ��tΪ��
��6-3����1
=3��1
=3���룩��
����F�͵�D���غ�ʱ��
��F���������ǣ�y=6��6=1��
����ƽ��ʱ��tΪ��
��6-1����1
=5��1
=5���룩��
����ͼ1����1��t��3ʱ��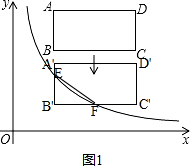 ��
��
B��F=$\frac{6}{4-t}$-2=$\frac{2t-2}{4-6}$��
B��E=2-��6-3-t��
=t-1
��S=$\frac{1}{2}��B��F��B��E$
=$\frac{1}{2}��t-1����\frac{2t-2}{4-t}$
=$\frac{{��t-1��}^{2}}{4-t}$
����ͼ2����3��t��5ʱ��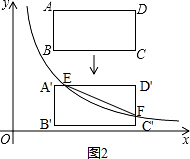 ��
��
ED��=6-$\frac{6}{6-t}$=$\frac{30-6t}{6-t}$��
D��F=6-t-1=5-t��
��S=2��4-$\frac{1}{2}��\frac{30-6t}{6-t}����5-t��$
=$\frac{{3��5-t��}^{2}}{6-t}$
���ϣ��ɵ�S=$\left\{\begin{array}{l}{\frac{{��t-1��}^{2}}{4-t}����1��t��3��}\\{\frac{{3��5-t��}^{2}}{6-t}����3��t��5��}\end{array}\right.$��
��3����ͼ3��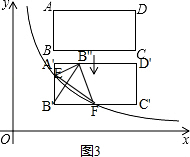 ��
��
���B�����EF�ĶԳƵ���B�壬��ʱEF��ֱ�߽���ʽ��y=k��x+b��
��E�������ǣ�2��$\frac{6}{2}$��������2��3����
�ѣ�2��3������y=k��x+b��
�ɵ�2k��+b=3����1����
EF��y=$\frac{k}{x}$������������E��F��E��2��3����
��F��������ǣ�x��y����
����$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=k��x+b}\end{array}\right.$��
�ɵ�k��x2+bx-6=0��
��2x=-$\frac{6}{k��}$��
���x=$-\frac{3}{k��}$��y=$\frac{6}{-\frac{3}{k��}}=-2k��$��
��F��������ǣ�-$\frac{k��}{3}��-2k��$����B��������ǣ�2��-2k�䣩��
��B��������ǣ�m��-2k��+2����
��$\frac{��2-2k�䣩-��-2k�䣩}{m-2}•k��=-1$��
���m=2-2k�䣬
��B��������ǣ�2-2k�䣬2-2k�䣩��
��EB���FB�壬
��$\frac{3-��2-2k�䣩}{2-��2-2k�䣩}•\frac{��2-2k�䣩-��2k�䣩}{��2-2k�䣩+\frac{3}{k��}}=-1$��
�������ɵ�k��2-2k��-2=0��
���k��=$1��\sqrt{3}$��
��k�䣼0��
��k��=1-$\sqrt{3}$��
��b=3-2��1-$\sqrt{3}$��=1$+2\sqrt{3}$��
��EF��ֱ�߽���ʽ�ǣ�
y=��1-$\sqrt{3}$��x$+��1+2\sqrt{3}��$��
���� ��1��������Ҫ�����˷����������ۺ��⣬�ô���ϵ�������������Ľ���ʽ�������˷������������������˷�������˼���Ӧ�ã�Ҫ�������գ�
��2����������˾��ε����ʡ�ƽ�Ƶ����ʵ�Ӧ�ã��Լ������ε����������ֱ�ߵĽ���ʽ����Ҫ�������գ�


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | ��$\sqrt{2}$ | C�� | $\root{3}{2}$ | D�� | -$\root{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
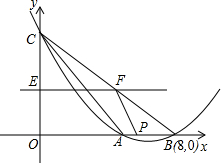 ��ͼ��������y=ax2+bx+c��a��0����x����A��B���㣬��y����C�㣬A����B�����࣬��֪B�������ǣ�8��0����tan��ABC=$\frac{1}{2}$����ABC�����Ϊ8��
��ͼ��������y=ax2+bx+c��a��0����x����A��B���㣬��y����C�㣬A����B�����࣬��֪B�������ǣ�8��0����tan��ABC=$\frac{1}{2}$����ABC�����Ϊ8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
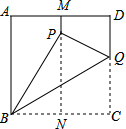 ��ͼ����һ�����Ϊ3��������ֽƬABCD��M��N�ֱ���AD��BC�ߵ��е㣬��C���۵���MN�ϣ�����P���λ�ã��ۺ�ΪBQ������PQ����PQ=1��
��ͼ����һ�����Ϊ3��������ֽƬABCD��M��N�ֱ���AD��BC�ߵ��е㣬��C���۵���MN�ϣ�����P���λ�ã��ۺ�ΪBQ������PQ����PQ=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
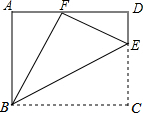 ��ͼ����E�Ǿ���ABCD��CD����һ�㣬��BCE��BE�۵�Ϊ��BFE����F����AD�ϣ���sin��DFE=$\frac{1}{3}$���� tan��EBC��ֵΪ$\frac{\sqrt{2}}{2}$��
��ͼ����E�Ǿ���ABCD��CD����һ�㣬��BCE��BE�۵�Ϊ��BFE����F����AD�ϣ���sin��DFE=$\frac{1}{3}$���� tan��EBC��ֵΪ$\frac{\sqrt{2}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
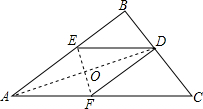 ��ͼ����������ֽƬABC�У���BACΪ��ǣ�AB=12cm��AC=15cm�������в����۵�����һ�Σ��ѡ�B�۵�ʹ��B����AC���ϣ��ۺ�ΪAD����BC�ڵ�D���ڶ����۵���ʹ��A���D�غϣ��ۺ۷ֱ�AB��AC�ڵ�E��F��EF��AD���ڵ�O��չ��������DE��DF��
��ͼ����������ֽƬABC�У���BACΪ��ǣ�AB=12cm��AC=15cm�������в����۵�����һ�Σ��ѡ�B�۵�ʹ��B����AC���ϣ��ۺ�ΪAD����BC�ڵ�D���ڶ����۵���ʹ��A���D�غϣ��ۺ۷ֱ�AB��AC�ڵ�E��F��EF��AD���ڵ�O��չ��������DE��DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
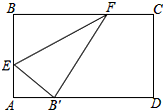 ��ͼ���۵�����ֽƬABCD��ʹ��B���ڱ�AD�ϣ��ۺ�EF�����˷ֱ���AB��BC�ϣ����˵㣩����AB=6cm��BC=10cm�����ۺ�EF�����ֵ��
��ͼ���۵�����ֽƬABCD��ʹ��B���ڱ�AD�ϣ��ۺ�EF�����˷ֱ���AB��BC�ϣ����˵㣩����AB=6cm��BC=10cm�����ۺ�EF�����ֵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com