
 如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.分析 (1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=$\frac{\sqrt{3}}{4}$,得到S△ACF=$\frac{\sqrt{3}}{4}$,通过△ACF∽△DAE,求得S△DAE=$\frac{9\sqrt{3}}{4}$,过A作AH⊥DE于H,解直角三角形得到AH=$\frac{\sqrt{3}}{3}$DH=$\frac{2\sqrt{3}}{3}$DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=$\frac{1}{2}$(180°-∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
解答 (1)证明:∵BC是⊙O的直径,
∴∠BAC=90°,
∵∠ABC=30°,
∴∠ACB=60°
∵OA=OC,
∴∠AOC=60°,
∵AF是⊙O的切线,
∴∠OAF=90°,
∴∠AFC=30°,
∵DE是⊙O的切线,
∴∠DBC=90°,
∴∠D=∠AFC=30°
∴∠DAE=∠ACF=120°,
∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,
∴∠CAF=30°,
∴∠CAF=∠AFC,
∴AC=CF
∴OC=CF,
∵S△AOC=$\frac{\sqrt{3}}{4}$,
∴S△ACF=$\frac{\sqrt{3}}{4}$,
∵∠ABC=∠AFC=30°,
∴AB=AF,
∵AB=$\frac{1}{2}$BD,
∴AF=$\frac{1}{2}$BD,
∴∠BAE=∠BEA=30°,
∴AB=BE=AF,
∴$\frac{AF}{DE}$=$\frac{1}{3}$,
∵△ACF∽△DAE,
∴$\frac{{S}_{△ACF}}{{S}_{△DAE}}$=($\frac{AF}{DE}$)2=$\frac{1}{9}$,
∴S△DAE=$\frac{9\sqrt{3}}{4}$,
过A作AH⊥DE于H,
∴AH=$\frac{\sqrt{3}}{3}$DH=$\frac{\sqrt{3}}{6}$DE,
∴S△ADE=$\frac{1}{2}$DE•AH=$\frac{1}{2}$×$\frac{\sqrt{3}}{6}$•DE2=$\frac{9\sqrt{3}}{4}$,
∴DE=$3\sqrt{3}$;
(3)∵∠EOF=∠AOB=120°,
在△AOF与△BOE中,$\left\{\begin{array}{l}{∠OBE=∠OAF}\\{∠OEB=∠AFO}\\{OA=OB}\end{array}\right.$,
∴△AOF≌△BEO,
∴OE=OF,
∴∠OFG=$\frac{1}{2}$(180°-∠EOF)=30°,
∴∠AFO=∠GFO,
过O作OG⊥EF于G,
∴∠OAF=∠OGF=90°,
在△AOF与△OGF中,$\left\{\begin{array}{l}{∠OAF=∠OGF}\\{∠AFO=∠GFO}\\{OF=OF}\end{array}\right.$,
∴△AOF≌△GOF,
∴OG=OA,
∴EF是⊙O的切线.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,切线的判定和性质,圆周角定理,直角三角形的性质,证得△ACF∽△DAE是解题的关键.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:解答题
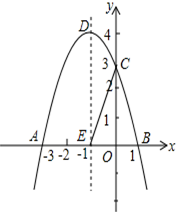 如图,关于y=-x2+bx+c的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,点E在x轴上.
如图,关于y=-x2+bx+c的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,点E在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-mx-3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
如图,抛物线y=x2-mx-3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
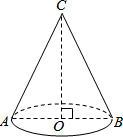 如图,一个圆锥形漏斗的底面半径OB=6cm,高OC=8cm.则这个圆锥漏斗的侧面积是( )
如图,一个圆锥形漏斗的底面半径OB=6cm,高OC=8cm.则这个圆锥漏斗的侧面积是( )| A. | 30cm2 | B. | 30πcm2 | C. | 60πcm2 | D. | 120cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
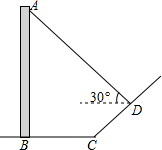 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
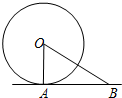 如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则AB的长为( )
如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则AB的长为( )| A. | 4$\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解飞行员视力的达标率应使用抽样调查 | |
| B. | 一组数据3,6,6,7,9的中位数是6 | |
| C. | 从2000名学生中选200名学生进行抽样调查,样本容量为2000 | |
| D. | 一组数据1,2,3,4,5的方差是10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com