
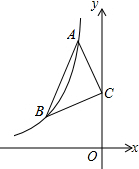
 如图,△ABC的顶点A,B都在反比例函数y=-$\frac{6}{x}$的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图,△ABC的顶点A,B都在反比例函数y=-$\frac{6}{x}$的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$. 分析 过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,-$\frac{6}{m}$),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入B点坐标即可得出点B的坐标,结合等腰直角三角形的性质以及两点间的距离公式即可得出结论.
解答 解:过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,如图所示.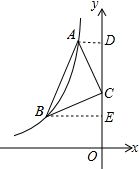 ∵∠ACB=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,$\left\{\begin{array}{l}{∠CAD=∠BCE}&{\;}\\{AC=CB}&{\;}\\{∠ACD=∠CBE}&{\;}\end{array}\right.$,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,-$\frac{6}{m}$)(m<0),
则E(0,-$\frac{6}{m}$),点D(0,3-m),点A(-$\frac{6}{m}$-3,3-m),
∵点A(-$\frac{6}{m}$-3,3-m)在反比例函数y=-$\frac{6}{x}$上,
∴3-m=-$\frac{6}{-\frac{6}{m}-3}$,
解得:m=-3,m=2(舍去).
∴点B的坐标为(-3,2),
∴AB=$\sqrt{2}$BC=$\sqrt{2}$$\sqrt{(-3-0)^{2}+(2-3)^{2}}$=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了反比例函数的性质、全等三角形的判定及性质、等腰直角三角形的性质以及两点间的距离公式,解题的关键是求出点B的坐标.本题属于基础题,难度不大,解决该题型题目时,设出反比例函数图象上一点的坐标,根据边角关系表示出来另一点的坐标,再结合点在反比例函数图象上得出点的坐标,最后由两点间的距离公式求出线段的长度即可.


科目:初中数学 来源: 题型:选择题
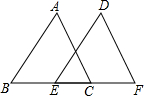 如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )
如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )| A. | ∠A=∠D | B. | DF∥AC | C. | AC=DF | D. | AB=DE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
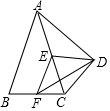 如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC的中点,连接EF,ED,FD.
如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC的中点,连接EF,ED,FD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
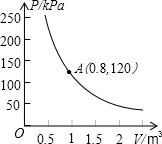 某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,则当气球内气体体积V(m3)的范围是0.8<V<2时,气体的压强p(kPa)的范围是48<p<120.
某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,则当气球内气体体积V(m3)的范围是0.8<V<2时,气体的压强p(kPa)的范围是48<p<120.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com