
【题目】已知二次函数y=(x﹣m)(x﹣m﹣4)(m为常数).
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)求证:不论m为何值,该函数的图象的顶点纵坐标不变;
(3)若该函数的图象与x轴交点为A、B,与y轴交点为C,当﹣3≤m≤﹣1时,△ABC面积S的取值范围为 .
【答案】(1)证明见解析;(2)证明见解析;(3)6≤S≤8.
【解析】
(1)当y=0时,(x-m)(x-m-4)=0,解得x1=m,x2=m+4,即可得到结论;
(2)图象与x轴的两个交点坐标为(m,0)、(m+4,0),由抛物线的对称性可知图象顶点横坐标为m+2,代入解析式求得y=-4,从而求得结论;
(3)当-3≤m≤-1时,求出S=2|m2+4m|,然后根据二次函数的性质求解即可.
(1)当y=0时,(x-m)(x-m-4)=0,
解得:x1=m,x2=m+4,
∵m≠m+4,方程有两个不相等的实数根,
∴不论m为何值,函数图象与x轴总有两个不同的公共点;
(2)由(1)得图象与x轴的两个交点坐标为(m,0)、(m+4,0),
由抛物线的对称性可知图象顶点横坐标为m+2,
把x=m+2代入y=(x﹣m)(x﹣m﹣4)得y=﹣4,
∴不论m为何值,该函数的图象的顶点纵坐标不变为﹣4;
(3)∵y=(x﹣m)(x﹣m﹣4)=x2﹣(2m+4)x+m2+4m,
∴C(0,m2+4m).
∵图象与x轴的两个交点坐标为(m,0)、(m+4,0),
∴AB=4,
∴S![]() ABOC
ABOC![]() ×|m2+4m|=2|m2+4m|,
×|m2+4m|=2|m2+4m|,
当m=﹣3时,S=2×3=6;当m=﹣1时,S=2×3=6,
当顶点在y轴上,即m=﹣2时,|m2+4m|最大值是4,故此时S=2×4=8,∴6≤S≤8.
故答案为:6≤S≤8.


科目:初中数学 来源: 题型:
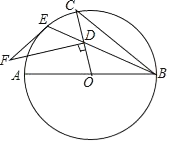
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
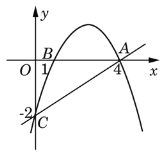
【题目】如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
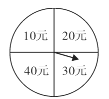
【题目】“十·一”期间,某服装店为了吸引更多的顾客购买服装,在.店门口设计了一个转转盘促销活动:当顾客转动转盘,根据指针指示返还相应的现金,若指针指在分界线时,需要重新转动,直到指向数字为止,购买几件服装就转动几次转盘.李女士购买了两件服装,她得到返还的现金数不低于![]() 元的概率是__________.
元的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
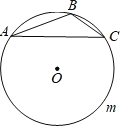
【题目】如图,△ABC中,∠ABC=120°,AC=2,⊙O是△ABC的外接圆,D是![]() 上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
上任意一点(不包括点A、C),顺次连接四边形ABCD四边中点得到四边形EFGH,则四边形EFGH的周长的最大值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
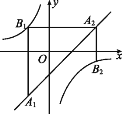
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为![]() (n为正整数).若
(n为正整数).若![]() ,则
,则![]() __,
__,![]() __.
__.
查看答案和解析>>
科目:初中数学 来源: 题型:
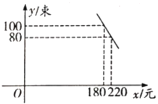
【题目】女本柔弱,为母则刚,说的是母亲对子女无私的爱,母爱伟大,值此母亲节来临之际,某花店推出一款康乃馨花束,经过近几年的市场调研发现,该花束在母亲节的销售量![]() (束)与销售单价
(束)与销售单价![]() (元)之间满足如图所示的一次函数关系,已知该花束的成本是每束100元.
(元)之间满足如图所示的一次函数关系,已知该花束的成本是每束100元.
(1)求出![]() 关于
关于![]() 的函数关系式(不要求写
的函数关系式(不要求写![]() 的取值范围);
的取值范围);
(2)设该花束在母亲节盈利为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数关系式:并求出当售价定为多少元时,利润最大?最大值是多少?
的函数关系式:并求出当售价定为多少元时,利润最大?最大值是多少?
(3)花店开拓新的进货渠道,以降低成本.预计在今后的销售中,母亲节期间该花束的销售量与销售单价仍存在(1)中的关系.若想实现销售单价为200元,且销售利润不低于9900元的销售目标,该花束每束的成本应不超过多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的日益提高,人们越来越喜欢过节,节日的仪式感日渐浓烈.某校举行了“女神节暖心特别行动”,从中随机调査了部分同学的暖心行动,并将其分为A,B,C,D四种类型(分别对应送服务、送鲜花、送红包、送话语).现根据调查的数据绘制成如下的条形统计图和扇形统计图.
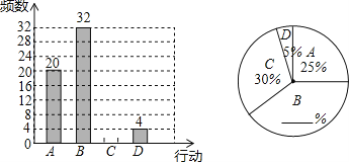
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校共抽查了多少名同学的暖心行动?
(2)补全条形统计图和扇形统计图;
(3)若该校共有2400名同学,请估计该校进行送鲜花行动的同学约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ).旋转后的菱形为
).旋转后的菱形为![]() .在旋转探究活动中提出下列问题,请你帮他们解决.
.在旋转探究活动中提出下列问题,请你帮他们解决.
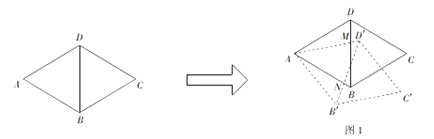
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .请说明线段
.请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
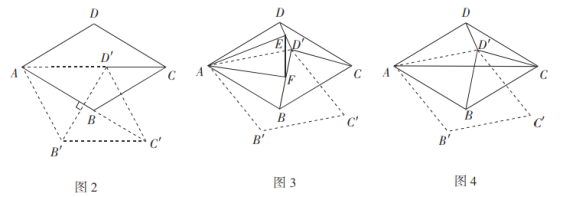
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时,![]() 的长为______;
的长为______;
(3)如图3,若旋转角为![]() 时,分别连接
时,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com