
【题目】(本题满分12分)如图,在平面直角坐标系xOy中,将抛物线![]() 的对称轴绕着点P(
的对称轴绕着点P(![]() ,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上的一点.
,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上的一点.
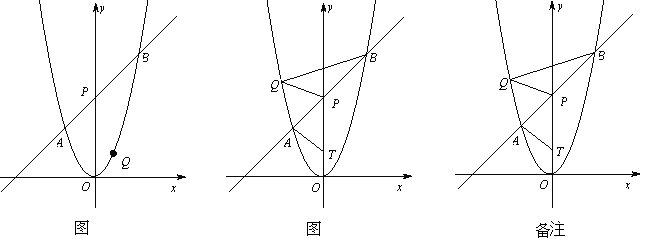
(1)求直线AB的函数表达式;
(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值;
(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是直线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值.
【答案】(1)y=x+2;
(2)当m=![]() 时,点Q到直线AB的距离的最大,最大距离为
时,点Q到直线AB的距离的最大,最大距离为![]() ;
;
(3)t=1或t=0或t=1-![]() 或t=3-
或t=3-![]() .
.
【解析】
试题分析:(1)根据题意求出直线AB与坐标轴的交点坐标,用待定系数法即可求解;(2)过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,设Q(m,m2),则C(m,m+2),用m表示出QC的长,再根据QC与QD的关系,构造QD与m的二次函数模型,利用二次函数的的性质即可求得点Q到直线AB的距离的最大值;(3)由题意可知∠APT=45°,△PBQ中必有一个内角等于45°,由图知∠BPQ=45°不合题意.分两种情况,①若∠PBQ=45°,可得BQ∥x轴,可证得△BPQ为等腰直角三角形,若△PAT与△BPQ相似,则△PAT也是等腰直角三角形,在分∠PAT为直角或∠PAT为直角两种情况求t值;②若∠PQB=45°,①中是情况之一,答案同上;现以点F为圆心,FB为半径作圆,则P、B、Q1都在⊙F上,设⊙F与y轴左侧的抛物线交于另一点Q2,根据圆周角定理可得∠PQ2B=∠PQ1B=45°,利用两边对应成比例且夹角相等的两个三角形相似,也分两种情况(i)△Q2PB∽△PAT,(ii)△Q2BP∽△PAT,根据三角形相似,利用相似的性质求t值.
试题解析:解:(1)设直线AB与x轴的交点为M,∵∠OPA=45°,
∴OM=OP=2,即点M的坐标为(-2,0).
设直线AB的函数解析式为y=kx+b,将M(-2,0)和P(![]() ,2)两点坐标代入,
,2)两点坐标代入,
得![]() ,解得
,解得![]() ,故直线AB的函数解析式为y=x+2.
,故直线AB的函数解析式为y=x+2.

过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,
根据条件可知△QDC为等腰直角三角形.
所以QD=![]() ,
,
设Q(m,m2),则C(m,m+2),
∴QC=m+2-m2=![]()
QD=![]() =
=![]() .
.
故当m=![]() 时,点Q到直线AB的距离的最大,最大距离为
时,点Q到直线AB的距离的最大,最大距离为![]() .
.

∵∠APT=45°,∴△PBQ中必有一个内角等于45°,由图知∠BPQ=45°不合题意.
①若∠PBQ=45°,过点B作x的平行线,与抛物线和y轴分别交于点Q、F,此时满足∠PBQ1=45°.
∵Q1(-2,4)、F(0,4),∴此时△BPQ1为等腰直角三角形,由题意可知△PAT也为等腰直角三角形.
(i)当∠PAT为直角时,得PT=AT=1,此时t=1;
(ii)当∠PAT为直角时,得PT=2,此时t=0.
②若∠PQB=45°,①中是情况之一,答案同上;
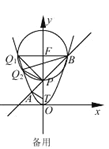
现以点F为圆心,FB为半径作圆,则P、B、Q1都在⊙F上,设⊙F与y轴左侧的抛物线交于另一点Q2,
∵∠PQ2B=∠PQ1B所对的弧相同,
∴∠PQ2B=∠PQ1B=45°.
即这里的交点Q2也符合要求.
设Q2(n,n2)(-2<n<0),由FQ2=2,得![]() ,
,
即![]() ,解得
,解得![]() ,
,
而-2<n<0,故n=![]() ,即Q2(
,即Q2(![]() ,3).
,3).
可证△PFQ2为等边三角形,所以∠PFQ2=60°,又弧PQ2=弧PQ2
所以∠PBQ2=![]() ∠PFQ2=30°,则在△PQ2B中,∠PQ2B=45°,∠PBQ2=30°.
∠PFQ2=30°,则在△PQ2B中,∠PQ2B=45°,∠PBQ2=30°.
(i)若△Q2PB∽△PAT,则过点A作y轴垂线,垂足为E.
则ET=![]() AE=
AE=![]() ,OE=1,∴OT=
,OE=1,∴OT=![]() -1,解得t=1-
-1,解得t=1-![]() .
.
(ii)若△Q2BP∽△PAT,则过点T作直线AB的垂线,垂足为G.
设TG=a,则PG=TG=a,AG=![]() TG=
TG=![]() a,AP=
a,AP=![]()
∴![]() a+a=
a+a=![]() ,解得PT=
,解得PT=![]() a=
a=![]() -1
-1
∴OT=OP-PT=3-![]() ,∴t=3-
,∴t=3-![]() .
.
综上所述,所求t的值为t=1或t=0或t=1-![]() 或t=3-
或t=3-![]() .
.


科目:初中数学 来源: 题型:
【题目】(知识回顾)
七年级学习代数式求值时,遇到这样一类题“代数式![]() 的值与
的值与![]() 的取值无关,求
的取值无关,求![]() 的值”,通常的解题方法是:把
的值”,通常的解题方法是:把![]() 、
、![]() 看作字母,
看作字母,![]() 看作系数合并同类项,因为代数式的值与
看作系数合并同类项,因为代数式的值与![]() 的取值无关,所以含
的取值无关,所以含![]() 项的系数为0,即原式=
项的系数为0,即原式=![]() ,所以
,所以![]() ,则
,则![]() .
.
(理解应用)
(1)若关于![]() 的多项式
的多项式![]() 的值与
的值与![]() 的取值无关,求m值;
的取值无关,求m值;
(2)已知![]() ,
,![]() ,且3A+6B的值与
,且3A+6B的值与![]() 无关,求
无关,求![]() 的值;
的值;
(能力提升)
(3)7张如图1的小长方形,长为![]() ,宽为
,宽为![]() ,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为
,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为![]() ,左下角的面积为
,左下角的面积为![]() ,当AB的长变化时,
,当AB的长变化时,![]() 的值始终保持不变,求
的值始终保持不变,求![]() 与
与![]() 的等量关系.
的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)(6x-1)2=25;
(2)x2-2x=2x-1;
(3)x2-![]() x=2;
x=2;
(4)x(x-7)=8(7-x).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省空间,家里的饭碗一般是竖直摆放的,如果![]() 只饭碗(形状、大小相同)竖直摆放的高度为
只饭碗(形状、大小相同)竖直摆放的高度为![]() 只饭碗竖直摆放的高度为
只饭碗竖直摆放的高度为![]() .如图所示,小颖家的碗橱每格的高度为
.如图所示,小颖家的碗橱每格的高度为![]() 则一摞碗竖直放人橱柜时,每格最多能放________________________.
则一摞碗竖直放人橱柜时,每格最多能放________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
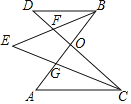
【题目】如图所示,AB、CD相交于点O,若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,∠A=45°,∠BEC=40°,则∠D的度数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
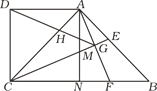
【题目】如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.

(1)若|x+2y-10|+|2x-y|=0,试分别求出1秒钟后△AOB的面积;
(2)如图2,所示,设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
(3)如图3所示,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,设∠AGH=α,∠BGC=β,试探究出α和β满足的数量关系并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠BAC=90°,AB=AC,点E为△ABC内一点,连接AE,CE,CE⊥AE,过点B作BD⊥AE,交AE的延长线于D.

(1)如图1,求证BD=AE;
(2)如图2,点H为BC中点,分别连接EH,DH,求∠EDH的度数;
(3)如图3,在(2)的条件下,点M为CH上的一点,连接EM,点F为EM的中点,连接FH,过点D作DG⊥FH,交FH的延长线于点G,若GH:FH=6:5,△FHM的面积为30,∠EHB=∠BHG,求线段EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
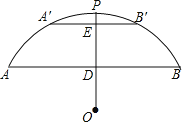
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com