Question

如图，在锐角三角形ABC中，，BC边上的高AM=6，D，E分别是边AB，AC上的两个动点（D不与，重合），且保持DE∥BC，以DE为边，在点的异侧作正方形DEFG．

（1）因为             ，所以△ADE∽△ABC．

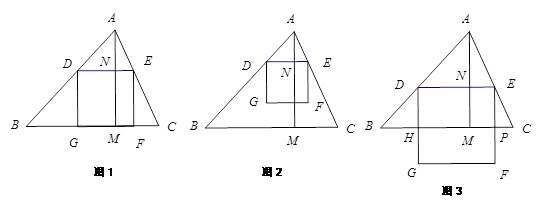
（2）如图1，当正方形DEFG的边GF在BC上时，求正方形DEFG的边长；

（3）设DE = x，△ABC与正方形DEFG重叠部分的面积为y．

①如图2，当正方形DEFG在△ABC的内部时，求关于的函数关系式，写出x的取值范围；

②如图3，当正方形DEFG的一部分在△ABC的外部时，求关于的函数关系式，写出x的取值范围；

③当x为何值时，y有最大值，最大值是多少？

 

Answer 1

 

（1）DE∥BC

（2）

（3）

①≤

②

③当时，有最大值为15

解析:解：（1）因为  DE∥BC    ， 所以△ADE∽△ABC……………2分

（2）当正方形DEFG的边GF在BC上时

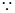△ADE∽△ABC,

∴………………………………………………4分

而AN=AM－MN=AM－DE，∴…………………5分

解之得……………………………………………………6分

∴当正方形DEFG的边GF在BC上时，正方形DEFG的边长为

（3）①当正方形DEFG在△ABC的内部时，△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积，

∵DE=x，∴……………………………………………………8分

此时x的范围是≤ …………………………………………9分

②当正方形DEFG的一部分在△ABC的外部时，

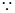△ADE∽△ABC,

∴，而AN=AM－MN=AM－EP,

∴，解得.

所以,  即………………………………11分

此时.………………………………………………………12分

③当≤时，△ABC与正方形DEFG重叠部分的面积的最大值

…………………………………………13分

当时，，

                 ＝

所以当时，有最大值为15………………………………14分

因为 14.062515

所以△ABC与正方形DEFG重叠部分的面积的最大值为15 …………15分