
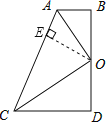
【题目】如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA平分∠BAC.
(1)求证:OC平分∠ACD;
(2)求证:OA⊥OC.

【答案】(1)见解析;(2)见解析
【解析】
(1)过点O作OE⊥AC于E,根据角平分线的性质可得OB=OE,求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明即可;
(2)利用“HL”证明△ABO和△AEO全等,可得∠AOB=∠AOE,同理∠COD=∠COE,然后求出∠AOC=90°,再根据垂直的定义即可证明.
证明:(1)过点O作OE⊥AC于E,
∵∠ABD=90°,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∵∠D=90°,
∴OD⊥CD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
![]() ,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理得:∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=![]() ×180°=90°,
×180°=90°,
∴OA⊥OC.


科目:初中数学 来源: 题型:
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)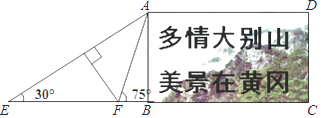
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).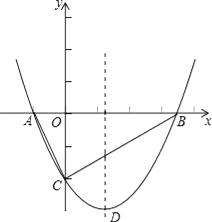
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、6,则四边形DHOG的面积是( )
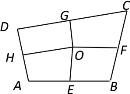
A. 5B. 4C. 8D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上由B出发向C点运动,同时点Q在线段CA上由C点出发向A点运动.设运动时间为t秒.
(1)若点P的速度为3cm/s,用含t的式子表示第t秒时,BP= cm,CP= cm.
(2)在(1)的条件下,若点Q运动速度与点P的运动速度相等,经过几秒钟△BPD与△CQP全等,说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,且点P的速度比点Q的速度慢1cm/s时,点Q的运动速度为多少时?能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是米. 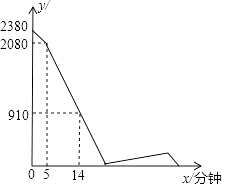
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知一次函数
中,已知一次函数![]() 的图像与
的图像与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.

(1)求点![]() 坐标和点
坐标和点![]() 坐标;
坐标;
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 为坐标原点,点
为坐标原点,点![]() 在第二象限,且四边形
在第二象限,且四边形![]() 为菱形,求点
为菱形,求点![]() 坐标;
坐标;
(3)在(2)的条件下,点![]() 为平面直角坐标系中一点,以
为平面直角坐标系中一点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出所有满足条件的
为顶点的四边形是平行四边形,请直接写出所有满足条件的![]() 点坐标.
点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com