
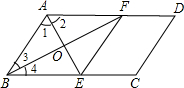
 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题:| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
科目:初中数学 来源: 题型:阅读理解
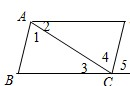 4、请阅读以下说明过程,并补全所空内容:
4、请阅读以下说明过程,并补全所空内容:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
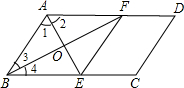 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: ∠BAF,∠3=∠4=
∠BAF,∠3=∠4= ∠ABE.
∠ABE. (∠BAF+∠ABE)=
(∠BAF+∠ABE)= ×180°=90°.
×180°=90°.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
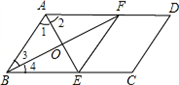
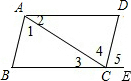
证明:(1)∵四边形ABCD是平行四边形,
(2)∴AD∥BC.
(3)∴∠ABE+∠BAF=180°.
(4)∵AE、BF分别平分∠BAF、∠ABE,
(5)∴∠1=∠2= ∠BAF,∠3=∠4=
∠BAF,∠3=∠4= ∠ABE.
∠ABE.
(6)∴∠1+∠3= (∠BAF+∠ABE)=
(∠BAF+∠ABE)= ×180°=90°.
×180°=90°.
(7)∴∠AOB=90°.
(8)∴AE⊥BF.
(9)∴四边形ABEF是菱形.
…
问:①上述说明过程是否正确?
答: _________ .
②如果错误,指出在第 _________ 步到第 _________ 步推理错误,应在第 _________ 步后添加如下证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com