
| ���� | 10��1�� | 10��2�� | 10��3�� | 10��4�� | 10��5�� | 10��6�� | 10��7�� |
| �����仯 �����ˣ� | +2.1 | +1.78 | +0.2 | -0.8 | -1 | -1.6 | -1.5 |
���� ��1��������������9��30�յ���������2.1��1.78���ɣ�
��2���ֱ�����ÿ������������������жϣ�
��3�����ݣ�2����8���������Ӽ��ɣ�
��� �⣺��1��3.9+2.1+1.78=7.78���ˣ�
��10��2�յ�����Ϊ7.78���ˣ�
��2��1�յ�����Ϊ��3.9+2.1=6���ˣ�
2�յ�����Ϊ��6+1.78=7.78���ˣ�
3�յ�����Ϊ��7.78-0.2=7.98���ˣ�
4�յ�����Ϊ��7.98-0.8=7.18���ˣ�
5�յ�����Ϊ��7.18-1=6.18���ˣ�
6�յ�����Ϊ��6.18-1.6=4.58���ˣ�
7�յ�����Ϊ��4.58-1.5=3.08���ˣ�
���Թ�������������ο�����������10��3�գ��ﵽ7.98���ˣ��ο��������ٵ���10��7�գ��ﵽ3.8���ˣ�
��3��6+7.78+7.98+7.18+6.18+4.58+3.08��43���ˣ�
�������ڹ������������һ���Ӵ���43�����οͣ�
�ʴ�Ϊ��7.78��3��7.98��7��3.8��
���� ���⿼���֪ʶ�������������������������㣬�ؼ�����ȷ����������ݵĺ��壬��ȷ�����ÿ���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��Ҫ��ͼ����գ���ͼAD��BC��AB��CD��
��Ҫ��ͼ����գ���ͼAD��BC��AB��CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��������������y=$\frac{k}{x}$��y=$\frac{1}{x}$�ڵ�һ�����ڣ���P��y=$\frac{k}{x}$��ͼ���ϣ�PC��ֱ��X���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A��PD��ֱ��Y����D����y=$\frac{1}{x}$��ͼ���ڵ�B������P��y=$\frac{k}{x}$��ͼ�����˶�ʱ�����н��۴�����ǣ�������
��������������y=$\frac{k}{x}$��y=$\frac{1}{x}$�ڵ�һ�����ڣ���P��y=$\frac{k}{x}$��ͼ���ϣ�PC��ֱ��X���ڵ�C����y=$\frac{1}{x}$��ͼ���ڵ�A��PD��ֱ��Y����D����y=$\frac{1}{x}$��ͼ���ڵ�B������P��y=$\frac{k}{x}$��ͼ�����˶�ʱ�����н��۴�����ǣ�������| A�� | ��ODB���OCA�������� | |
| B�� | ����A��PC���е�ʱ����Bһ����PD���е� | |
| C�� | ֻ�е��ı���OCPBΪ������ʱ���ı���PAOB�������� | |
| D�� | $\frac{CA}{PA}$=$\frac{DB}{PB}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a+3b=5ab | B�� | 3a2+2a3=5a5 | C�� | 6ab-ab=5ab | D�� | 5+a=5a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{2}$ | B�� | $\frac{5\sqrt{3}}{2}$ | C�� | 5 | D�� | 5$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
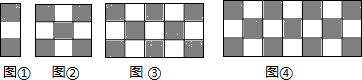
| A�� | 3n-1 | B�� | 3n+1 | C�� | 4n-1 | D�� | 4n+1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com