
【题目】如图所示,正比例函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]()
![]() 在第一象限的图象交于点
在第一象限的图象交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的垂线,垂足为
轴的垂线,垂足为 ![]() ,已知△OAM的面积为1.
,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且点
不重合),且点 ![]() 的横坐标为1,在
的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
【答案】
(1)解:设A点的坐标为( ![]() ,
, ![]() ),
),
则 ![]() .∴
.∴ ![]() .
.
∵ ![]() ,∴
,∴ ![]() .∴
.∴ ![]() .
.
∴反比例函数的解析式为 ![]()
(2)解: 由 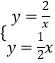 得
得 ![]() 或
或 ![]() ∴A为
∴A为 ![]() .
.
设A点关于 ![]() 轴的对称点为C,则C点的坐标为
轴的对称点为C,则C点的坐标为 ![]() .
.
如要在 ![]() 轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
令直线BC的解析式为 ![]() .
.
∵B为(1,2),∴ ![]() ∴
∴ ![]()
∴BC的解析式为 ![]() .
.
当 ![]() 时,
时, ![]() .∴P点坐标为
.∴P点坐标为 ![]() .
.
【解析】(1)根据反比例函数k的几何意义,由已知△OAM的面积为1,设A点的坐标为( a , b ),得出![]() a b = 1,即可求出k(k>0)的值,从而得出反比例函数的解析式。
a b = 1,即可求出k(k>0)的值,从而得出反比例函数的解析式。
(2)此题是在 x 轴上求一点 P ,使 P A + P B 最小,根据轴对称的性质,先作出A点关于 x 轴的对称点为C,连接BC交x轴于点P,可得出点C的坐标,再求出直线BC的函数解析式,根据y=0,求出对应的自变量的值,即可得出点P的坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OD平分∠BOC,OE平分∠AOC,则下列说法错误的是( )

A. ∠DOE为直角B. ∠DOC和∠AOE互余
C. ∠AOD和∠DOC互补D. ∠AOE和∠BOC互补
查看答案和解析>>
科目:初中数学 来源: 题型:
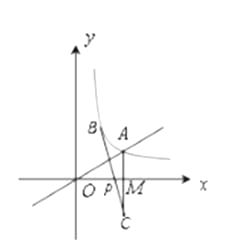
【题目】如图:抛物线y=- ![]() +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC=
+bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= ![]() ,tanα-tanβ=2,∠ACB=90°.
,tanα-tanβ=2,∠ACB=90°.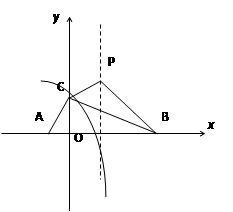
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把直线y=﹣2x向上平移后,分别交y轴、x轴于A、B两点,直线AB经过点(m,n)且2m+n=6,则点O到线段AB的距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, ![]() 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).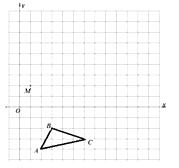
①画出△ABC关于 ![]() 轴对称的△A1B1C1;
轴对称的△A1B1C1;
②以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 , 使△A2B2C2与△A1B1C1的相似比为2︰1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: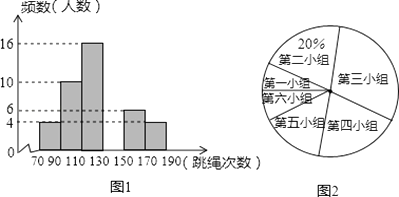
(1)补全频数分布直方图 , 并指出这个样本数据的中位数落在第小组;(1)
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同的数字的卡片,请你按要求抽出卡片,完成下列各问题:
![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最大,最大值是 ;
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,最小值是 ;
(3)从中取出4张卡片,用学过的运算方法,使结果为24.写出运算式子:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读短文,然后回答短文后面所给出的问题:
对于三个数a、b、c的平均数,最小的数都可以给出符号来表示,我们规定M{a,b,c}表示a,b,c这三个数的平均数,min{a,b,c}表示a,b,c这三个数中最小的数,max{a,b,c}表示a,b,c这三个数中最大的数.例如:M{﹣1,2,3}=![]() ,min{﹣1,2,3}=﹣1,max{﹣1,2,3}=3;M{﹣1,2,a}=
,min{﹣1,2,3}=﹣1,max{﹣1,2,3}=3;M{﹣1,2,a}=![]() ,min{﹣1,2,a}=
,min{﹣1,2,a}=![]() .
.
(1)请填空:max{c﹣1,c,c+1}= ;若m<0,n>0,min{3m,(n+3)m,﹣mn}= ;
(2)若min{2,2x+2,4﹣2x}=2,求x的取值范围;
(3)若M{2,x+1,2x}=min{2,x+1,2x},求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,BC=![]() ,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
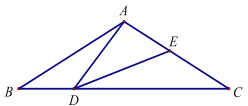
(1)求证:∠BAD∠EDC;
(2)当BD= 时,△ABD≌△EDC,并说明理由.
(3)当△ADE是直角三角形时,求AD的长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com