
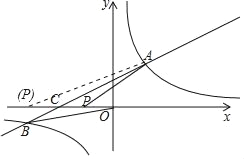
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

【答案】(1)![]() ;(2)(-6,0)(-2,0)
;(2)(-6,0)(-2,0)
【解析】分析:(1)利用反比例函数图象上点的坐标特征可求出点A、B的坐标,再利用待定系数法即可求出直线AB的解析式;
(2)利用一次函数图象上点的坐标特征可求出点C的坐标,设点P的坐标为(x,0),根据三角形的面积公式结合S△ACP=![]() S△BOC,即可得出|x+4|=2,解之即可得出结论.
S△BOC,即可得出|x+4|=2,解之即可得出结论.
详解:(1)∵点A(m,3),B(﹣6,n)在双曲线y=![]() 上,
上,
∴m=2,n=﹣1,
∴A(2,3),B(﹣6,﹣1).
将(2,3),B(﹣6,﹣1)代入y=kx+b,
得:![]() ,解得
,解得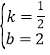 .
.
∴直线的解析式为y=![]() x+2.
x+2.
(2)当y=![]() x+2=0时,x=﹣4,
x+2=0时,x=﹣4,
∴点C(﹣4,0).
设点P的坐标为(x,0),
∵S△ACP=![]() S△BOC,A(2,3),B(﹣6,﹣1),
S△BOC,A(2,3),B(﹣6,﹣1),
∴![]() ×3|x﹣(﹣4)|=
×3|x﹣(﹣4)|=![]() ×
×![]() ×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,
×|0﹣(﹣4)|×|﹣1|,即|x+4|=2,
解得:x1=﹣6,x2=﹣2.
∴点P的坐标为(﹣6,0)或(﹣2,0).


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
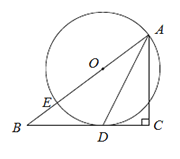
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
【1】求a的值;
【2】求A,B的坐标;
【3】以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光小区附近有一块长100m,宽80m的长方形空地,在空地上有两条相同宽度的步道(一纵一横)和一个边长为步道宽度7倍的正方形休闲广场,两条步道的总面积与正方形休闲广场的面积相等,如图1所示.设步道的宽为a(m).

(1)求步道的宽.
(2)为了方便市民进行跑步健身,现按如图2所示方案增建塑胶跑道.己知塑胶跑道的宽为1m,长方形区域甲的面积比长方形区域乙大441m2, 且区域丙为正方形,求塑胶跑道的总面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,它从A处出发去看望B,C,D格点处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B![]() 从B到A记为B→A
从B到A记为B→A![]() 其中第一个数表示左右方向移动,第二个数表示上下方向移动.
其中第一个数表示左右方向移动,第二个数表示上下方向移动.

(1)图中A→C![]() C→D
C→D![]()
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)若图中格点处另有两只甲虫M,N.且M→A![]() M→N
M→N![]() ,则N→A应记为什么?直接写出答案.
,则N→A应记为什么?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组![]() 的解是 ;
的解是 ;
(2)a= ;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)|﹣3|﹣5×(﹣![]() )+(﹣4)
)+(﹣4)
(2)(﹣2)2﹣4÷(﹣![]() )+(﹣1)2016
)+(﹣1)2016
(3)![]() ×(﹣24)
×(﹣24)
(4)﹣12014﹣(1﹣0.5)÷![]() ×[(﹣2)3﹣4]
×[(﹣2)3﹣4]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为300,测得大楼顶端 A的仰角为450(点B,C,E在同一水平直线上)。已知AB=50m,DE=10m,求障碍物B,C两点间的距离。(结果精确到1m,参考数据: ![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com