
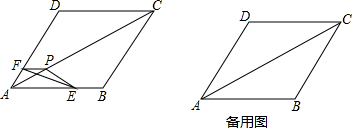
分析 (1)根据锐角三角函数求出∠FPG,最后求出∠EPF.
(2)先判断出Rt△PME≌Rt△PNF,再根据锐角三角函数求解即可,
(3)根据运动情况及菱形的性质判断求出AP最大和最小值.
解答 解:(1)过点P作PG⊥EF于点G,如图1所示.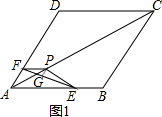
∵PE=PF=6,EF=6 $\sqrt{3}$,
∴FG=EG=3 $\sqrt{3}$,∠FPG=∠EPG=$\frac{1}{2}$∠EPF.
在Rt△FPG中,sin∠FPG=$\frac{FG}{PF}$=$\frac{3\sqrt{3}}{6}$=$\frac{\sqrt{3}}{2}$,
∴∠FPG=60°,
∴∠EPF=120°.
(2)过点P作PM⊥AB于点M,作PN⊥AD于点N,如图2所示.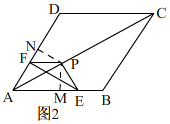
∵AC为菱形ABCD的对角线,
∴∠DAC=∠BAC,AM=AN,PM=PN.
在Rt△PME和Rt△PNF中,PM=PN,PE=PF,
∴Rt△PME≌Rt△PNF,
∴ME=NF.
又AP=10,∠PAM=$\frac{1}{2}$∠DAB=30°,
∴AM=AN=APcos30°=10×$\frac{\sqrt{3}}{2}$=5 $\sqrt{3}$,
∴AE+AF=(AM+ME)+(AN-NF)=AM+AN=10 $\sqrt{3}$.
(3)如图,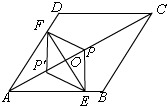
当点P在EF右边时,
∵∠BAD=60°,∠EPF=120°,
∴∠BAD+∠EPF=180°,
∴点A,E,P,F四点共圆,
∴AP是此圆的直径时,AP最大,
∵PE=PF,
∴EF⊥AC时,AP最大,
∴当EF⊥AC,点P在EF的右侧时,AP有最大值,
同理:当EF⊥AC,点P在EF的左侧时,AP有最小值,
设AC与EF交于点O,
∵PE=PF,
∴OF=$\frac{1}{2}$EF=3 $\sqrt{3}$,
∵∠FPA=60°,
∴OP=3,
∵∠BAD=60°,
∴∠FAO=30°,
∴AO=9,
∴AP=AO+PO=12,
同理AP′=AO-OP=6,
∴AP的最大值为12,AP的最小值为6,
点评 本题考查菱形的性质、等腰三角形的性质、角平分线的性质定理、垂线段最短、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
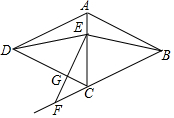 如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,
如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com