
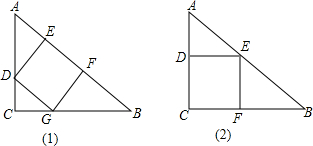
分析 如图(1),利用三角形的面积关系求出AB边上的高,再利用相似三角形的性质求出正方形的边长;
如图(2),设出正方形的边长,再利用相似三角形的性质求出正方形的边长.
边长≥17cm的正方形符合题意.
解答  解:如图(1),因为△ABC为直角三角形,边长分别为30cm和40cm,则AB=$\sqrt{3{0}^{2}+4{0}^{2}}$=50(cm).
解:如图(1),因为△ABC为直角三角形,边长分别为30cm和40cm,则AB=$\sqrt{3{0}^{2}+4{0}^{2}}$=50(cm).
作AB边上的高CH,交DG于点Q.
于是$\frac{2CH}{5}$=$\frac{30×40}{2}$,
故CH=24cm.
易得:△DCG∽△ACB,
故:$\frac{CQ}{CH}$=$\frac{DG}{AB}$.
设正方形DEFG的边长为xcm,
得:$\frac{24-x}{24}$=$\frac{x}{50}$,
解得:x=$\frac{600}{37}$<17,不合题意,舍去.
如图(2),令AC=3cm,设正方形边长为ycm.
易得:△ADE∽△ACB,
于是:$\frac{AD}{AC}$=$\frac{DE}{CB}$,
$\frac{30-y}{30}$=$\frac{y}{40}$,
解得:y=$\frac{120}{7}$>17.符合题意.
综上所述,第二种方法合乎要求.
点评 本题考查了相似三角形的应用.(1)利用面积法求出直角三角形斜边上的高是解答此题的关键;(2)可根据△ADE∽△ACB或△BFE∽△BCA来解答.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:选择题
| A. | 只有①正确 | B. | 只有②正确 | C. | ①,②都不正确 | D. | ①、②都正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com