
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
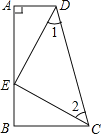
(1)求证:△ADE≌△BEC;
(2)若AD=3,AB=9,求△ECD的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据已知可得到∠A=∠B=90°,DE=CE,AD=BE从而利用HL判定两三角形全等;
(2)由三角形全等可得到对应角相等,对应边相等,由已知可推出∠DEC=90°,由已知我们可求得BE、AE的长,再利用勾股定理求得ED的长,利用三角形面积公式解答即可.
(1)∵AD∥BC,∠A=90°,∠1=∠2,
∴∠A=∠B=90°,DE=CE.
∵AD=BE,
在Rt△ADE与Rt△BEC中
![]() ,
,
∴Rt△ADE≌Rt△BEC(HL)
(2)由△ADE≌△BEC得∠AED=∠BCE,AD=BE.
∴∠AED+∠BEC=∠BCE+∠BEC=90°.
∴∠DEC=90°.
又∵AD=3,AB=9,
∴BE=AD=3,AE=9﹣3=6.
∵∠1=∠2,
∴ED=EC=![]() =
=![]() =3
=3![]() ,
,
∴△CDE的面积=![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16,AD是BC边上的中线且AD=6,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).

A.![]() B.16C.6D.10
B.16C.6D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆.若三角形为锐角三角形,则其最小覆盖圆为其外接圆;若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.问题:能覆盖住边长为![]() 、
、![]() 、
、![]() 的三角形的最小圆的直径是________.
的三角形的最小圆的直径是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
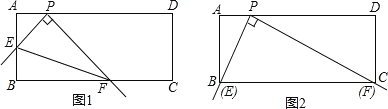
【题目】在矩形ABCD中,点P在AD上,AB=![]() ,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).当点E与点B重合时,点F恰好与点C重合(如图2).将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径长为.
,AP=1.将直角尺的顶点放在P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).当点E与点B重合时,点F恰好与点C重合(如图2).将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中,从开始到停止,线段EF的中点所经过的路径长为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x22(k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
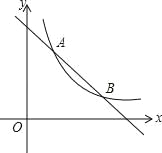
【题目】如图,一次函数 y=﹣x+4 的图象与反比例 y=![]() (k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(1)求点 A、B 的坐标及反比例函数的表达式;
(2)在 x 轴上找一点,使 PA+PB 的值最小,求满足条件的点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的高,
边上的高,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)联结![]() 、
、![]() ,猜想
,猜想![]() 与
与![]() 之间的关系,并写出推理过程;
之间的关系,并写出推理过程;
(3)若将锐角![]() 变为钝角
变为钝角![]() ,如图(2),上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
,如图(2),上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,外出旅游的人数逐渐增多,对旅行包的需求也将增多,某店准备到生产厂家购买旅行包,该厂有甲、乙两种新型旅行包.若购进10个甲种旅行包和20个乙种旅行包共需5600元,若购进20个甲种旅行包和10个乙种旅行包共需5200元.
(1)甲、乙两种旅行包的进价分别是多少元?
(2)若该店恰好用了7000元购买旅行包;
①设该店购买了m个甲种旅行包,求该店购买乙种旅行包的个数;
②若该店将甲种旅行包的售价定为298元,乙种旅行包的售价定为325元,则当该店怎么样进货,才能获得最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识重现)我们知道,在ax=N中,已知底数a,指数x,求幂N的运算叫做乘方运算.例如23=8;已知幂N,指数x,求底数a的运算叫做开方运算,例如![]() =2;
=2;
(学习新知)
现定义:如果ax=N(a>0且a≠1),即a的x次方等于N(a>0且a≠1),那么数x叫做以a为底N的对数(logarithm),记作x=logaN.其中a叫做对数的底数,N叫做真数,x叫做以a为底N的对数.例如log28=3.零没有对数;在实数范围内,负数没有对数.
(应用新知)
(1)填空:在ax=N,已知幂N,底数a(a>0且a≠1),求指数x的运算叫做_____运算;
(2)选择题:在式子log5125中,真数是_____
A.3 B.5 C.10 D.125
(3)①计算以下各对数的值:log39;log327;log3243.
②根据①中计算结果,请你直接写出logaM,logaN,loga(MN)之间的关系.(其中a>0且a≠1,M>0,N>0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com