
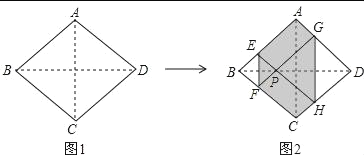
【题目】如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2),设AE=x(0<x<2),给出下列判断:①x=![]() 时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
A.①②B.①③C.②D.②③
【答案】C
【解析】
由折叠的性质和正方形的性质可得四边形BEPF,四边形PGDH是正方形,四边形AEPG,四边形PFCH是矩形,可得AE=PG=GD=DH=PH=FC,BE=BF=EP=PF=AG=CH,即可判断①②③.
∵折叠,
∴BE=EP,BF=PF,∠ABC=∠EPF=90°,
∵BD平分∠ABC,EF垂直平分BP,
∴BE=BF,
∴四边形BEPF是菱形,且∠EBF=90°,
∴四边形BEPF是正方形,
同理四边形PGDH是正方形,
∴∠AGP=90°,∠AEP=90°,
∴四边形AEPG是矩形,
同理四边形CFPH是矩形,
∴AE=PG=GD=DH=PH=FC,BE=BF=EP=PF=AG=CH,
当x=![]() ,则BE=
,则BE=![]() ,
,
∴EF=![]() ,
,
∴AB+EF=2+![]() ,
,
∵AB=BC=2,
∴AC=2![]()
∴AB+EF<AC,
故①错误;
∵六边形AEFCHG周长=AE+AG+CH+CF+EF+GH=AE+BE+CF+BF+![]() BE+
BE+![]() AE,
AE,
∴六边形AEFCHG周长=AB+BC+![]() (AE+BE)=4+2
(AE+BE)=4+2![]() 是定值,
是定值,
故②正确;
∵六边形AEFCHG面积=2×2﹣![]() BE2﹣
BE2﹣![]() GD2=4﹣
GD2=4﹣![]() (EP2+AE2)=4﹣
(EP2+AE2)=4﹣![]() EG2
EG2
∴六边形AEFCHG面积不是定值,
故③错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点横坐标是2,与x轴交于A(x1,0)、
图象的顶点横坐标是2,与x轴交于A(x1,0)、
B(x2,0),x1﹤0﹤x2,与y轴交于点C,O为坐标原点,![]() .
.
(1)求证:![]() ;
;
(2)求m、n的值;
(3)当p﹥0且二次函数图象与直线![]() 仅有一个交点时,求二次函数的最大值.
仅有一个交点时,求二次函数的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 30 | 40 | 60 |
周销售量y(件) | 90 | 70 | 30 |
周销售利润w(元) | 450 | 1050 | 1050 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)当售价定为多少时,周销售利润最大,最大利润是多少?
(3)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过45元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1080元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为16元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)如果厂商每月的制造成本不超过480万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
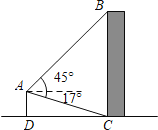
【题目】一夜之间,新冠病毒肺炎席卷全球。疫情期间,我国为保障大家的健康,各地采取了多种方式预防。其中,某地运用无人机规劝居民回家。如图,无人机于空中 A 处测得某建筑顶部 B 处的仰角为 45°,测得该建筑底部 C 处的俯角为 17°.若无人机的飞行高度 AD 为 62m,求该建筑的高度 BC .(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=4,矩形DEFG的顶点D、G分别在AC、BC上,边EF在AB上.
(1)求证:△AED∽△DCG;
(2)若矩形DEFG的面积为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
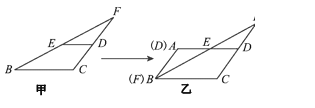
【题目】如图甲,已知ED是△FBC的中位线,沿线段ED将△FED剪下后拼接在图乙中△BEA的位置.
(1)从△FED到△BEA的图形变换,可以认为是(填平移或轴对称或旋转)变换;
(2)试判断图乙中四边形ABCD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的不等式组 有且只有四个整数解,又关于x的分式方程
有且只有四个整数解,又关于x的分式方程![]() ﹣2=
﹣2=![]() 有正数解,则满足条件的整数k的和为( )
有正数解,则满足条件的整数k的和为( )
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a<0)经过点A、B.
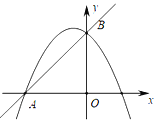
(1)求a、b满足的关系式及c的值.
(2)当x<0时,若y=ax2+bx+c(a<0)的函数值随x的增大而增大,求a的取值范围.
(3)如图,当a=﹣1时,在抛物线上是否存在点P,使△PAB的面积为1?若存在,请求出符合条件的所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com